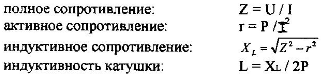Что такое активное сопротивление катушки

Активное сопротивление катушки

Активное сопротивление обуславливается омической характеристикой проводов обмотки. При работе на низких частотах, омическое сопротивление не зависит от частоты. В мощных устройствах необходимо учитывать эффект близости, который заключается в том, что токи и образуемое ими магнитное поле вызывают вытеснение тока в проводах соседних витков. В результате, снижается эффективное используемое сечение провода и растет его омическое сопротивление.

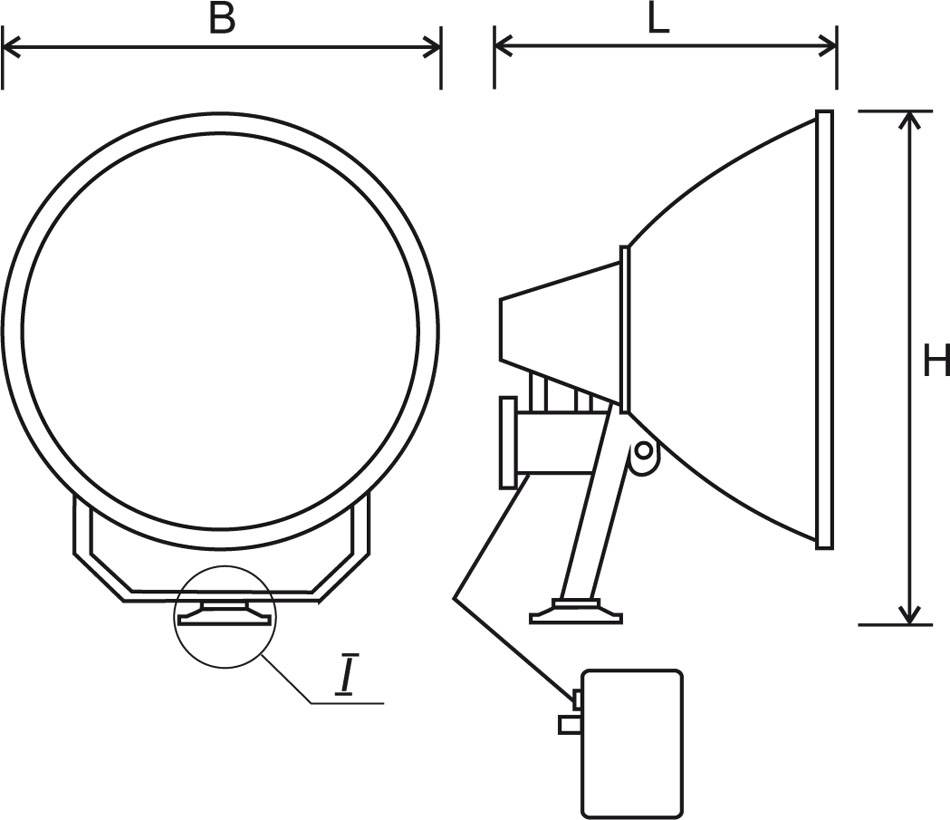
Обратите внимание! На высоких частотах проявляется скин-эффект, который заключается в том, что ток вытесняется в поверхностные слои провода. В результате этого снижается используемое сечение кабеля

Для снижения скин-эффекта вместо одного проводника используют жгут из нескольких более тонких – литцендрат, либо поверхность провода покрывают слоем серебра, поскольку оно обладает наименьшим удельным сопротивлением.

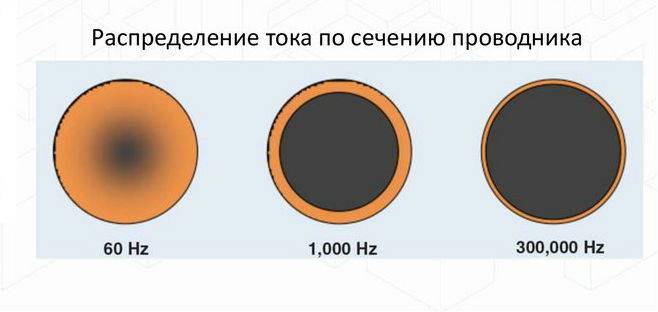Скин-эффект

В мощных электромагнитных системах (ускорители частиц) для снижения активного сопротивления, используется свойство сверхпроводимости – полное исчезновение сопротивления при охлаждении некоторых материалов ниже критической температуры.

Провод литцендрат

Во многих случаях применения катушек индуктивности следует учитывать влияние активного сопротивления обмоток. Данный параметр может отрицательно влиять не только путем снижения добротности, но и вызывать повышенный нагрев проводников обмоток в том случае, когда устройство работает с большими токами.

Конструкция и разновидности

Все типы катушек индуктивности имеют одинаковую конструкцию, независимо от области их использования. Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.

1. Соленоид. Компонент с увеличенной общей длиной обмоточного провода. Обмотка больше диаметра детали.
2. Тороидальная. В такой катушке соленоид выполнен в форме «тора».
3. Многослойный тип, имеет несколько рядов обмотки.
4. Секционированная. Обмотка имеет несколько разделенных секций, иногда из провода разного сечения. Наиболее известной катушкой этого типа является трансформатор или дроссель.
5. Универсальная, может совмещать сразу несколько вариантов обмотки.

Независимо от конструкции, все катушки работают по одному и тому же принципу.

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

• L — индуктивность контура (в генри);
• Ф — величина магнитного потока, измеряемого в веберах;
• I — сила тока в катушке (в амперах).

Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

• µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
• N — количество витков в катушке;
• S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
• l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

• W — энергия магнитного потока, измеряемая в джоулях;
• I — сила тока в амперах.

Катушка с тороидальным сердечником

В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

• N — число витков катушки;
• µ — относительная магнитная проницаемость;
• µ0 — магнитная постоянная;
• S — площадь сечения сердечника;
• π — математическая постоянная, равная 3,14;
• r — средний радиус тора.

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

• l — длина проводника в метрах;
• r — радиус сечения провода, измеряемый в метрах;
• µ0 — магнитная постоянная;
• µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
• µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
• π — число Пи;
• ln — обозначение логарифма.

Активное сопротивление

При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, обратно в электрическую энергию не превращается. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.

Отличительной чертой элементов имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле

Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.

Какие отличия

Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.

Индуктивная величина и ее формулы

Важно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть. Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть

То есть, в окружающую среду полученная энергия не передается

Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.

Вам это будет интересно Особенности электрических мощностей

Комплексная сопротивляемость отдельного элетроэлемента сети R

В активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.

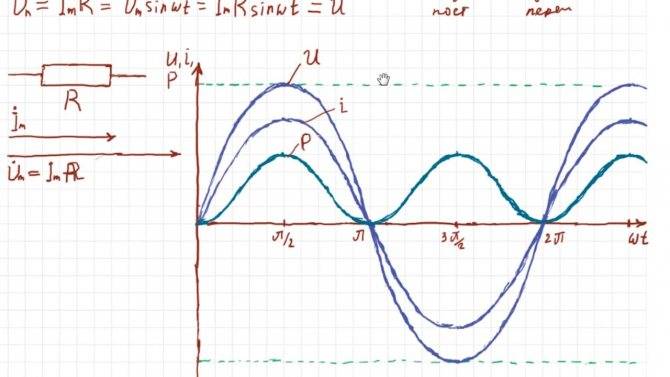
Активная сопротивляемость в цепи переменного синусоидального тока

Различия между активным и реактивным сопротивлением

Разница между активным и реактивным сопротивлением состоит в том, что при прохождении электротока по компонентам цепи, несущим активную нагрузку, имеют место мощностные потери в виде выделения тепла, которое не может быть снова превращено в электрическую энергию. В качестве наглядного примера можно привести конфорку электроплиты, выделяющую тепловую энергию. Такими свойствами обладают и осветительные устройства, электрические двигатели, различные кабели. Фазы проходящих через такие компоненты напряжения и электротока будут совпадать.

Внутреннее сопротивление – формула

Реактивные нагрузки отличаются наличием емкостных свойств либо способностью к индукции. В первом случае величина рассматриваемого сопротивления зависит от емкости, во втором – от электродвижущей силы самоиндукции.

Важно! Величина, в противоположность активной, может иметь плюсовой и минусовой знаки. Это зависит от того, в какую сторону идет фазовый сдвиг

При опережении электрическим током напряжения будет иметь место отрицательный показатель, в обратном случае – положительный.

Как определить сопротивление обмоток дросселя?

Сопротивление обмотки дросселя R определяется длинной провода катушки, зависящей от размеров сердечника, количества витков провода и удельного сопротивления проводника

где w – количество витков провода,

lcp – средняя длина витка провода,

Sпр – площадь поперечного сечения провода,

qпр – удельное электрическое сопротивление вещества провода.

Для определения средней длины витка в случае цилиндрического сердечника можно по следующей формуле

где Dc – диаметр каркаса, на который наматывается обмотка дросселя или, в случае бескаркасной намотки – диаметр сердечника,

m – число слоёв намотки,

dи – диаметр провода с изоляцией. Отмечу, что маркировка провода и идет без учёта изоляции, обычно толщина изоляции составляет 0,03…0,1 мм.

В случае прямоугольного сердечника или каркаса средняя длина витка в обмотке составляет

где а, b – стороны прямоугольника образующего сечение сердечника дросселя,

m – число слоёв намотки,

dи – диаметр провода с изоляцией.

В случае, если необходимо учесть изменение сопротивления провода из-за изменения температуры, необходимо внести поправку на повышение температуры

где R20 – сопротивление провода при температуре 20 °С (стандартная температура, при которой нормируется удельное сопротивление веществ), считается по вышеизложенной формуле,

α – температурный коэффициент сопротивления,

Т – температура до которой нагрелся проводник,

20 – стандартная температура, при которой нормируется удельное сопротивление веществ.

Данные выражения позволяют вычислить сопротивление обмотки дросселя при постоянном токе или токе низкой частоты, однако уже на частотах выше 1 кГц активное сопротивление начинает заметно расти, вследствие поверхностного эффекта (скин-эффект) и влияния соседних проводников обмотки (эффект близости). Для учёта роста сопротивления ввели добавочный коэффициент kд, который показывает во сколько раз сопротивление на данной частоте больше, чем сопротивление при постоянном токе. Тогда сопротивление обмоток дросселя на заданной частоте вычисляется по следующему выражению

где RПТ – сопротивление обмотки дросселя при постоянном токе,

kд – коэффициент добавочных потерь.

Коэффициент добавочных потерь зависит от глубины скин-слоя и количества слоёв дросселя. Глубина скин-слоя определяется следующим выражение

где f – частота переменного тока,

μа – абсолютная магнитная проницаемость вещества проводника,

ρ – удельное электрическое сопротивление.

Таким образом, в одиночном проводнике ток на высокой частоте протекает по внешней части проводника. Однако в катушке близко лежащие витки вытесняют ток на внешнюю часть обмотки, и в этом случае сопротивление проводника ещё больше увеличивается и зависит от количества слоев в обмотке дросселя, причём с ростом числа слоёв сопротивление первого слоя возрастает.

Для определения коэффициента добавочных потерь на сопротивление обмоток дросселя можно воспользоваться следующей формулой

где δ – глубина скин-слоя,

h – высота одного слоя,

m – количество слоёв в обмотке дросселя,

sinh и cosh – гиперболические синус и косинус.

Гиперболические функции могут быть преобразованы к следующему виду

В выражении для вычисления коэффициента добавочных потерь, значение высоты одного слоя соответствует квадратным проводникам расположенным «виток к витку», однако в большинстве случаев провод из которого мотается дроссель круглого сечения или состоит из нескольких свитых вместе проводников – литцендрата. Таким образом, необходимо диаметр проводника преобразовать к эквивалентной высоте слоя hэ

где d – диаметр проводника,

p – расстояние между центрами проводников.

В случае использования многожильного провода (литцендрата), выражение для коэффициента добавочных потерь будет иметь вид

где mэ – эквивалентное количество слоёв,

n – количество жил в многожильном проводе (литцендрат).

Необходимо отметить, что использование провода определённого диаметра или многожильного провода необходимо оценивать в ходе проверочных расчётов. А в общем случае необходимо снижать количество слоёв обмотки дросселя.

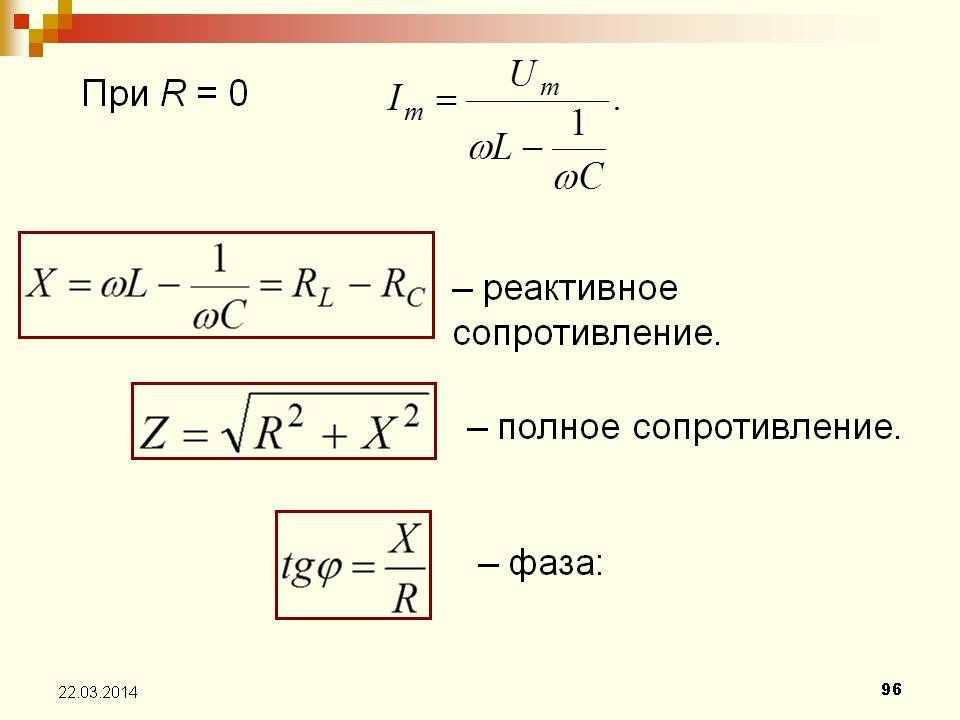
Формула расчета реактивного сопротивления

В общем случае для деталей катушечного типа применяются выражения:

X = L*w = 2* π*f*L.

Для конденсаторов применяют формулы:

X = 1/(w*C)= 1/(2* π*f*C).

Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.

Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.

Активное сопротивление

И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента  — резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим.  Как нам говорит вики-словарь, «активный  — это деятельный, энергичный, проявляющий инициативу». Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.

То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.

Виды пассивных элементов

Эквивалентное сопротивление

Данные устройства характеризуются тем, что вместо рассеивания энергии склонны к ее накоплению. Разные типы таких деталей создают различные формы сопротивления.

Катушка индуктивности

Это радиокомпонент, представляющий собой проводниковый элемент спиральной или винтообразной формы, покрытый изоляцией. В схемах катушки используют для нивелирования помех и искажений, снижения величины переменного тока, генерации магнитного поля. Длинные тонкие элементы носят название соленоидов. Катушки отличаются небольшими величинами активной сопротивляемости и емкости, но обладают индуктивностью, генерируя электродвижущую силу.

Подключение катушки в электрическую цепь

Емкостной элемент

Примером этого вида деталей является конденсатор. Он включает в себя две проводящие обкладки, между которыми находится диэлектрический материал. Протекание электротока обусловлено накоплением и отдачей обкладками своего заряда.

Подсоединение конденсатора в электроцепь

Индуктивное сопротивление катушки

Сопротивление тока: формула

Катушка индуктивности – пассивный компонент электросхем, который имеет возможность сохранять электроэнергию посредством превращения ее в магнитное поле. Такой процесс является главной функцией такого электрического компонента.

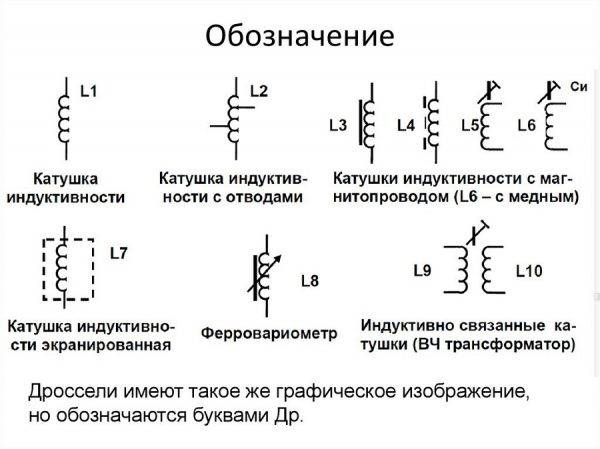
Разновидности обозначения катушек индуктивности на электросхемах

По своим свойствам и основным техническим характеристикам индуктивная катушка напоминает конденсатор, какой преобразует энергию в электрополе.

Индуктивность заключается в том, что вокруг проводникового элемента с током образуется магнитное поле. Связано это с ЭДС, что противодействует силе тока и приложенному электронапряжению в катушке. Это свойство есть индуктивное сопротивление катушки. Ее индуктивность можно увеличить посредством увеличения количества витков в ней.

Внешний вид сверхмощной катушки индуктивности

Интересно знать. Согласно закону Ома, сила электротока обратно пропорциональна сопротивлению и прямо пропорциональна электронапряжению в цепи. Если принять сопротивление катушки току переменного типа за величину ωL, то получится закон Ома для электрической цепи с чистой индуктивной нагрузкой. Формула будет выглядеть так: U0=I0*ωL.

Для выяснения количественной характеристики индуктивного сопротивления катушки стоит помнить, что оно противодействует электротоку переменного типа. На практике же индуктивная катушка имеет свое собственное некоторое сопротивление.

Переменный синусоидальный электроток, проходящий через катушку, приводит к возникновению ЭДС, или синусоидального электронапряжения переменного типа

Зная такое важное понятие, как индуктивное сопротивление, а также формулы и зависимости этой величины, можно производить верные расчеты во многих отраслях промышленности, электротехнике и энергетике

Мощность катушки

Треугольники напряжений, сопротивлений, мощностей

Цепь с реальной катушкой индуктивности

Реальная катушка отличается от идеальной тем, что переменный ток в ней сопровождается не только изменением энергии в магнит­ном поле, но и преобразованием электрической энергии в другой вид.

В цепи переменного тока процесс пре­образования электрической энергии в другой вид характеризуется активной мощностью цепи Р

, а изменение энергии в маг­нитном поле — реактивной мощностью. В реальной ка­тушке имеют место оба процесса, т.е. ее активная и реактивная мощности отличны от нуля. Поэтому в схеме замещения реальная катушка должна быть представлена активным и реактивным эле­ментами.

Приложенное к катушке напряжение состоит из двух слагаемых, одно из которых uR

равно падению напряжения в активном сопротивлении, а другоеuL уравновешивает ЭДС самоиндукции.

Поэтому катушку в схеме замещения можно пред­ставить активным и индуктивным сопротивлениями, соединенны­ми последовательно.

Несовпадение по фазе слагаемых в выражении затрудня­ет определение амплитуды и действующего значения приложенного к цепи напряжения U.

Поэтому воспользуемся векторным спосо­бом сложения синусоидальных величин. За исходный вектор диаграммы принимаем вектор тока I. На­правление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы. ВекторU Rпо направлению совпадает с вектором тока I, а вектор ULнаправлен перпендикулярно вектору I с положительным углом.Из диаграммы видно, что вектор общего напряжения Uопережа­ет вектор тока I на угол ψ> 0, но <90°, а по величине равен гипоте­нузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротив­лениях.

Проекция вектора напряжения Uна направление вектора тока называется активной составляющей вектора напряжения и обозна­чается UR.

Проекция вектора напряжения Uна направление, перпендику­лярное вектору тока, называется реактивной составляющей векто­ра напряжения.

Стороны треугольника напряжений, выраженные в единицах на­пряжения, разделим на ток I. Получим подобный треугольник со­противлений,катетами которого являются активное ииндуктивное сопротивления, а гипотенузой — величина Z. ; ;

Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи.

Из графика мгновенной мощности видно, что в тече­ние периода мощность четыре раза меняет знак; следовательно, на­правление потока энергии и в данном случае в течение периода меняется.

При положительном значе­нии мощности энергия пере­ходит от источника в прием­ник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, по­ступившей в приемник (положительная площадь), больше возвра­щенной обратно (отрицательная площадь).

Следовательно, в цепи с активным сопротивлением и индуктив­ностью часть энергии, поступающей от генератора, необратимо пре­вращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энер­гии в другой вид энергии (активная энергия) часть ее совершает ко­лебания между источником и приемником (реактивная энергия).

Скорость необратимого процесса преобразования энергии оцени­вается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощно­стью Q.

Активная мощность всей цепи равна активной мощности в сопро­тивлении R,

а реактивная — реактивной мощности в индуктивном со­противленииXL.,

Коэффициент мощности — показывает, какая часть пол­ной мощности является активной, т.е. потребляемой.

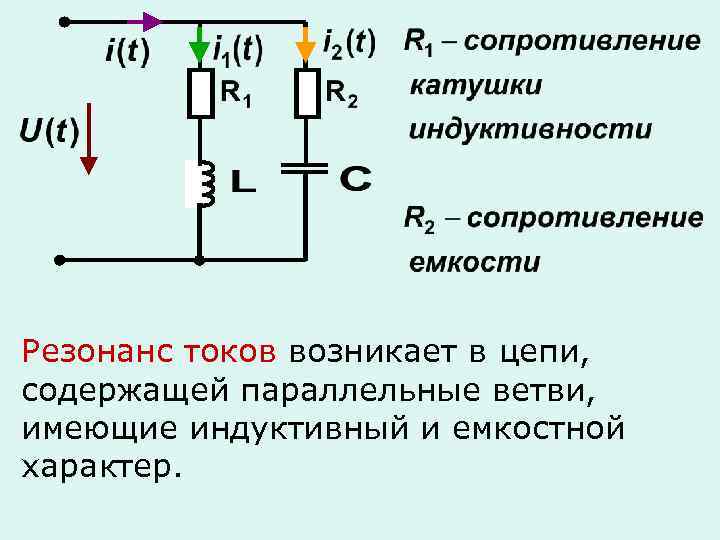
Схема замещения катушки с параллельным соединением элементов

Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G

и индуктивнойBL проводимостями.

Покажем, что схемы эквивалентны, то есть при одинаковом напряжении сохраняются не­изменнымиток в неразветвленной части цепи, активная и реактивная мощности.

; ;

Проекция вектора тока I на направление напряжения называет­ся активной составляющей вектора тока и обозначается Ia.

Проекция вектора тока I на направление, перпендикулярное век­тору напряжения, называется реактивной составляющей вектора тока и обозначается Iр=

Стороны треугольника токов, выраженные в единицах тока, мож­но разделить на напряжение U

и получить подобный треугольник проводимостей, катетами которого являются активнаяG ииндуктивнаяBL проводимости, а гипотенузой — величинаY= I/U, называемая полной проводимостью цепи.

Расчет параметров катушки

Приходится при расчётах рассматривать разные варианты. Расчет индуктивности зависит от исходных данных и заданных конечных параметров.

Расчет L в зависимости от заданной конструкции

Если исходными параметрами являются: w, D каркаса и длина намотанного провода, то формула для расчёта имеет вид:

L = 0,01*D*w2/(l/D) + 0,46,

где:

• D – диаметр каркаса, см;
• w – число витков;
• l – длина намотки, см;
• L – индуктивность, мкГн.

Подставляя численные значения в формулу, получают значение L.

Расчет количества витков по индуктивности

Зная D каркаса и L, рассчитывают количество витков в катушке, формула имеет вид:

w = 32*√(L*D),

где:

• L – индуктивность, мкГн;
• D – диаметр каркаса, мм.

Если в качестве исходных параметров берутся длина навитого в ряд проводника и его диаметр, то количество витков находят, используя формулу:

w = l/d,

где:

• l – длина намотки, мм;
• d – диаметр провода, мм.

Измерения диаметра провода проводят линейкой или штангенциркулем.

Расчёт индуктивности прямого провода

Собираясь найти L круглого прямого проводника, обращаются к приближённой формуле:

L = (μ0/2π)*l*( μe*ln(l/r) + 1/4* μi,

где:

• μ0 – магнитная постоянная;
• μe – относительная магнитная проницаемость (ОМП) среды (для вакуума – 1);
• μi – ОМП проводника;
• l – длина провода;
• r – радиус провода.

Формула справедлива для длинного проводника.

Расчёт однослойной намотки

Однослойные дроссели без сердечника легко и быстро можно рассчитать при помощи онлайн-калькулятора, в окно которого можно забить все известные характеристики, и программа выдаст значение L.

Вычисления проводятся и вручную, с использованием математического выражения. Оно имеет вид:

L = D2*n2/45D + 100*l,

где:

• D – диаметр катушки, см;
• l – длина намотанного провода, см;
• n – количество витков.

Формула подходит для вычислений L дросселей без ферритовых сердечников.

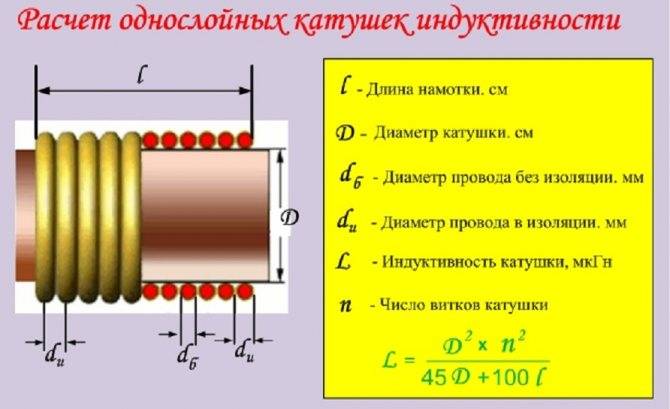
Однослойная катушка виток к витку

Дроссель с сердечником

При наличии сердечника следует учесть его размеры и форму. В случае одинаковых катушках индуктивность больше у той, которая располагается на сердечнике.

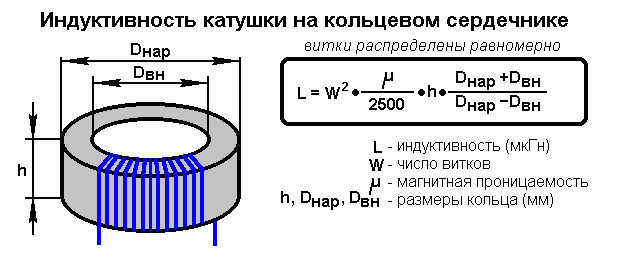
Расчёт однослойной намотки с сердечником

Многослойная намотка

Особенности расчёта при подобном способе наматывания провода заключаются в том, что нужно учитывать его толщину. Формула для дросселя без сердечника имеет вид:

N²=(L*(3Dk+9l+10t))/0.008Dk²,

где:

• Dk – общий диаметр (диаметр каркаса и намотки);
• t – толщина слоя;
• l – длина накрученного провода.

Все значения подставляют в мм, величину L – в мкГн.

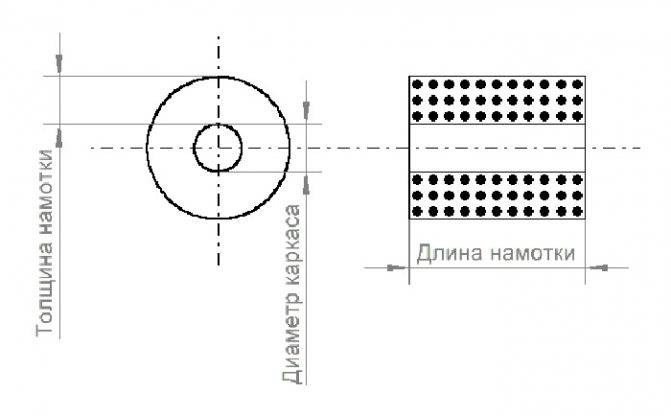
Многослойная намотка

Свойства ёмкостей

Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.

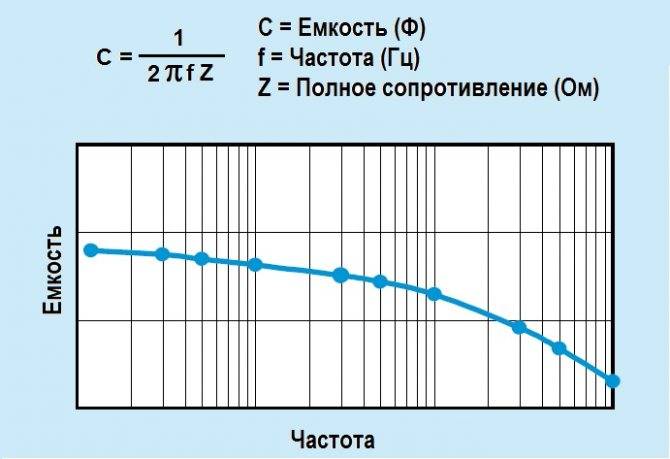
Свойства ёмкостей.

Здесь U – напряжение источника питания. Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.

Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.

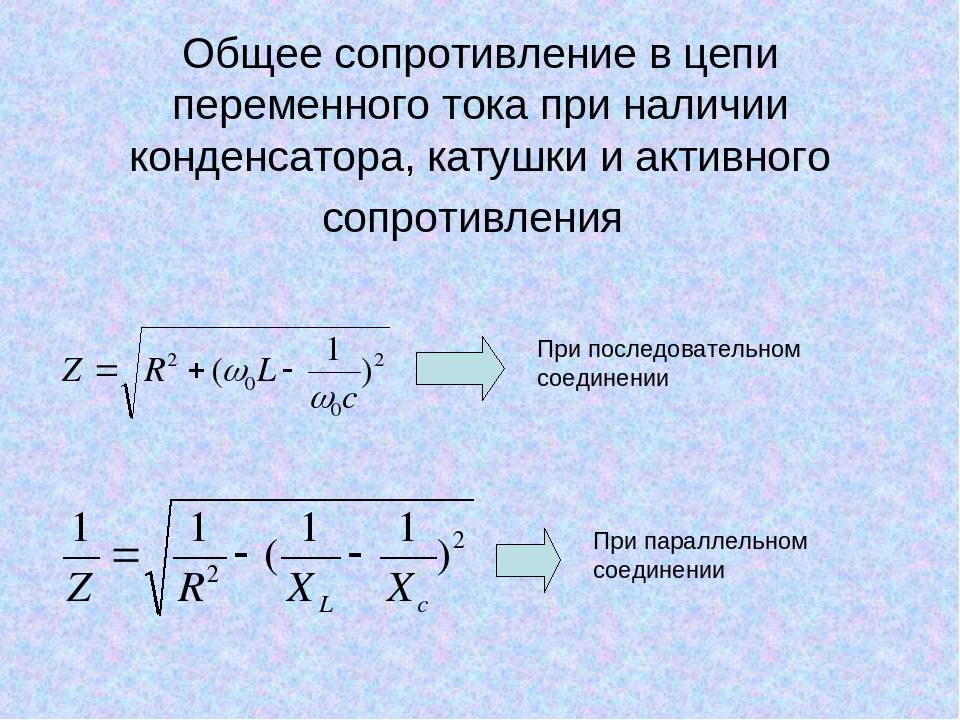
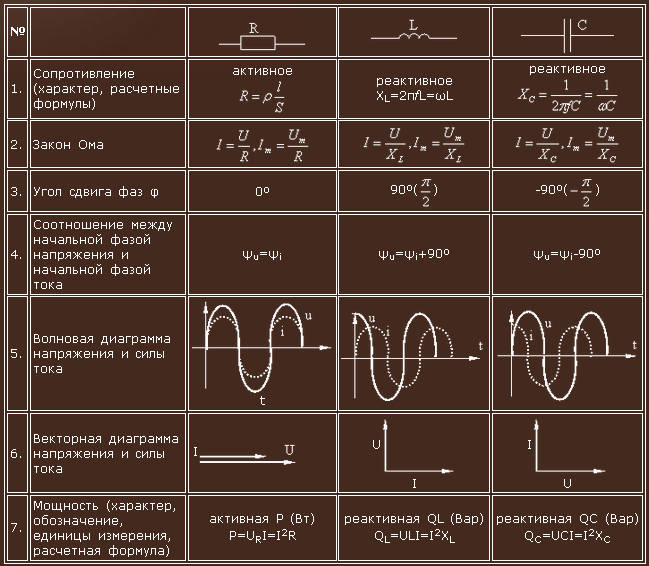
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением. В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:

Расчет сопротивления.

В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.

Будет интересно Конденсатор — простыми словами о сложном

Z = R + i X , где Z – импеданс, R – величина активного сопротивления , X – величина реактивного сопротивления, i – мнимая единица . В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:

• X > 0 – элемент проявляет свойства индуктивности .
• X = 0 – элемент имеет чисто активное сопротивление .
• X < 0 – элемент проявляет ёмкостные свойства.

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений.

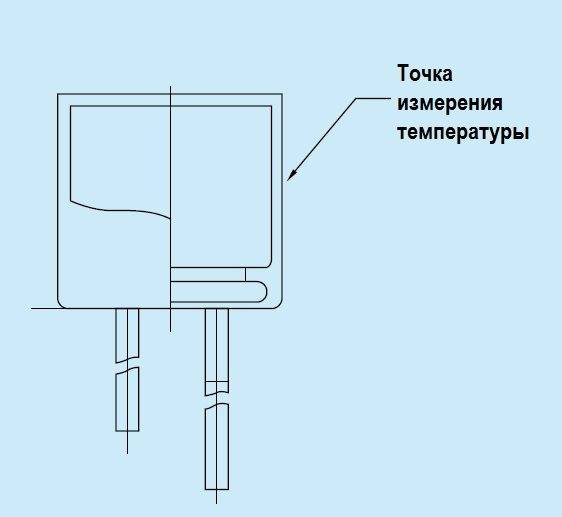
Индуктивное сопротивление (X L ) обусловлено возникновением ЭДС самоиндукции . Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.