Что такое ПИД регулятор для чайников?

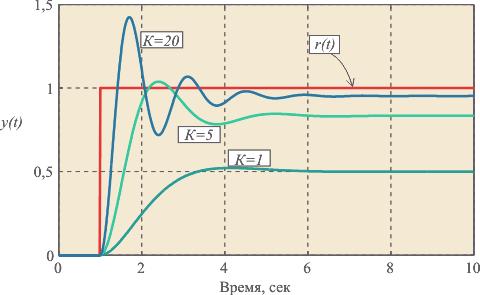
Методика настройки ПИД-регулятора

Выбор алгоритма управления и его  настройка является основной задачей в процессе проектирования и последующего удовлетворительного запуска агрегата в промышленную или иную эксплуатацию.

В основе методики лежит закон Циглера-Никольса, являющийся эмпирическим и основанным на использовании данных, полученных экспериментально на реальном объекте.

В результате ознакомления с методикой, а также при близком рассмотрении объектов регулирования, были выбраны формулы и коэффициенты ближе всего подходящие к реальному объекту регулирования.

Объект регулирования – камерная электрическая печь. Число зон регулирования от 24 до 40. Каждая зона есть набор электронагревателей. Материал нагревателей нихром. Тип —  проволочные, навитые на керамические трубки.

Требования: поддержание температуры по зонам печи +/- 5С.

МЕТОДИКА:

 Настройка пропорциональной компоненты (Xp)

1. Перед настройкой зоны пропорциональности интегральная и дифференциальная компоненты отключаются:

• Постоянная интегрирования устанавливается минимально возможной (Ти =0),
• Постоянная дифференцирования минимально возможной (Тд = 0).

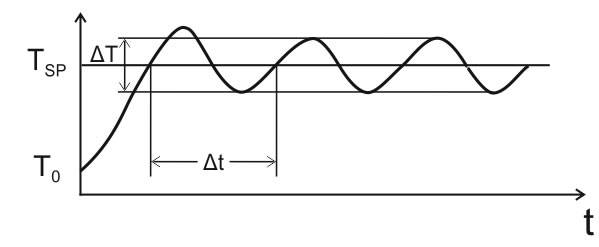
Тο — начальная температура в системе;
Тsp — заданная температура (уставка);
∆T — размах колебаний температуры;
∆t — период колебаний температуры.

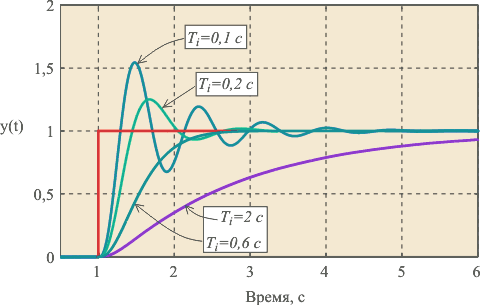
1. Меняем значение пропорциональной составляющей Xp от минимума (0) до момента, пока не появятся устойчивые колебания системы с периодом ∆t.

Система должна находится в постоянном колебательном процессе, притом колебательный процесс незатухающий, где ∆T– характеристика колебания равная значению величины рассогласования (±10С, или как по заданию). Колебания должны быть одинаковы от Тsp.

После получения данной кривой на нашем объекте, засекаем время периода колебаний ʌt – полный период. Данное время есть характеристика системы, оборудования.

3. Используя полученные параметры рассчитываем Ти и Тд.

	Зона пропорциональности	Коэффициент передачи	Постоянная времени интегрирования	Постоянная времени дифференцирования
П-регулятор	2*PBs	0.5*Xp
ПИ-регулятор	2.2*PBs	0.45*Xp	0.83*ʌТ
ПИД-регулятор	1.67*PBs	0.6*Xp	0.5*ʌТ	0.125*ʌТ

Цифры в формулах для расчета коэффициентов ПИД-регулирования скорректированы на основе запуска камерной электрической печи в опытно-промышленную эксплуатацию. И конечно в зависимости от типа объекта регулирования могут незначительно меняться.

Программа регулятор

Цифровой регулятор – это программа,
которая управляет некоторым процессом
(регулирует). Получая входные данные с
датчиков, она рассчитывает управляющее
воздействие, обычно это некоторое число,
которое в итоге с помощью электронной
схемы преобразуется в реальное физическое
воздействие. Задача регулятора — выйти
на заданные показатели датчиков.

Допустим некий прибор на основе
микроконтроллера должен регулировать
температуру жала паяльника. К прибору
подключён датчик температуры жала,
который точно показывает текущую
температуру жала — T_тек. Ну а
пользователь прибора задаёт нужную
температуру жала Т_зад , которую
прибор и должен поддерживать. Вот
типичная задача регулирования. Попробуем
самостоятельно придумать программу
регулятор температуры жала для этого
прибора.

Самое простое, что приходит в голову
каждому, это включать паяльник когда
заданная температура больше текущей и
выключать когда меньше. Данный регулятор
очень простой, он получает на входе
текущую температуру паяльника, заданную
температуру и возвращает число 1
(включить) или 0 (выключить паяльник).
Далее микроконтроллер преобразует это
число в высокий или низкий уровень
напряжения на выводе и управляет
паяльником. Это и есть программа
регулятор – вполне рабочий вариант.
Посмотрим какие у него есть минусы.

Так как прибор цифровой, то все в нем
работает по «часам». Датчик температуры
выдаёт данные только через какой-то
интервал времени. Пусть это будет один
раз в секунду. Теперь опишем свойства
самого паяльника. При включении паяльника
на полную мощность он нагревается за
одну секунду на 20 градусов, а остывает
за 1 сек на 5 градусов. В таком случае,
температура паяльника будет колебаться
около заданной +/- 20 градусов.

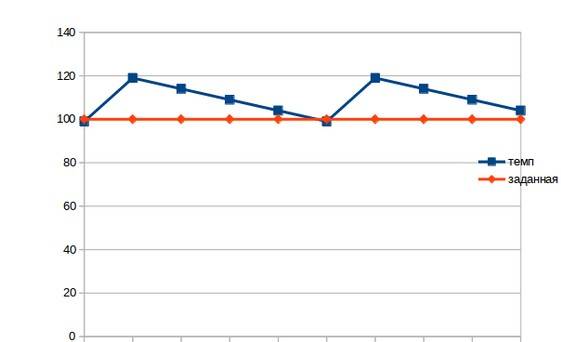
Почему так происходит? Как только мы
включим паяльник, через одну секунду
он добавит 20 градусов к своей температуре,
ещё до того как мы узнаем, что эта самая
температура превысила заданную. А потом
будет долго остывать. Чтобы сделать
реакцию паяльника более плавной, нужно
управлять не просто включением его на
полную мощность, а иметь возможно
регулировать эту мощность. И вот тут
как раз и нужен будет ПИД регулятор.

Настройка регулятора

Для настройки регулятора нужно варьировать коэффициенты:

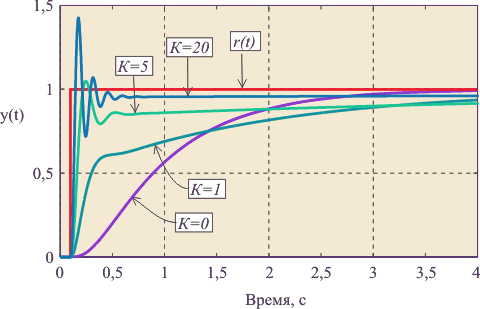
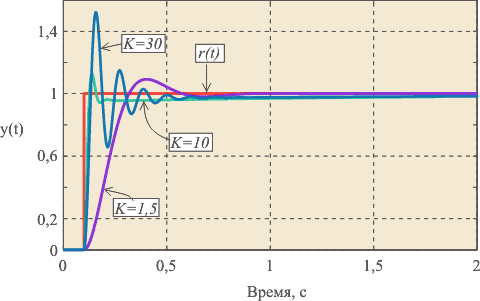
• При увеличении kP увеличивается скорость выхода на установленное значение, увеличивается управляющий сигнал. Чисто математически система не может прийти ровно к заданному значению, так как при приближении к установке П составляющая пропорционально уменьшается. При дальнейшем увеличении kP реальная система теряет устойчивость и начинаются колебания.
• При увеличении kI растёт скорость компенсации накопившейся ошибки, что позволяет вывести систему точно к заданному значению с течением времени. Если система медленная, а kI слишком большой – интегральная сумма сильно вырастет и произойдёт перерегулирование, которое может иметь характер незатухающих колебаний с большим периодом. Поэтому интегральную сумму в алгоритме регулятора часто ограничивают, чтобы она не могла увеличиваться и уменьшаться до бесконечности.
• При увеличении kD растёт стабильность системы, она не даёт системе меняться слишком быстро. В то же время kD может стать причиной неадекватного поведения системы и постоянных скачков управляющего сигнала, если значение с датчика шумит. На каждое резкое изменение сигнала с датчика Д составляющая будет реагировать изменением управляющего сигнала, поэтому сигнал с датчика нужно фильтровать (читай урок по фильтрам).

Вот так выглядит процесс стабилизации при изменении коэффициентов: 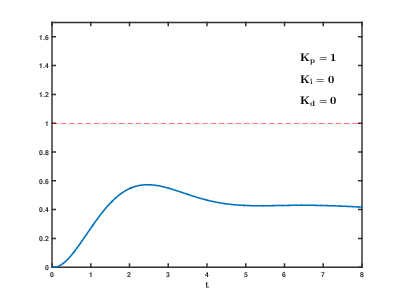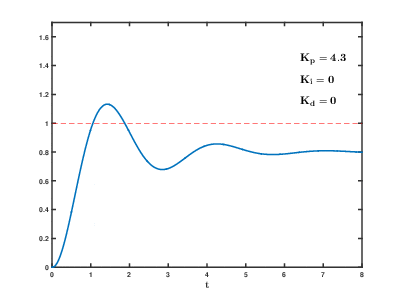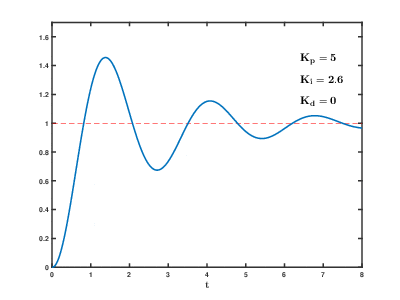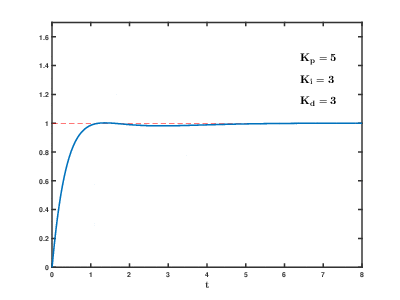  Настройка регулятора – дело не очень простое. Начальные коэффициенты для подбора можно получить по следующему алгоритму: сначала выставляем все коэффициенты в . Плавно увеличиваем kP до появления незатухающих колебаний. Значение kP, при котором они появились, запишем и обозначим как kP1. Далее замеряем период колебаний системы в секундах, обозначим как T. Итоговые коэффициенты получим так:

• kP = 0.6 * kP1
• kI = kP / T * 2 * dt
• kD = kP * T / 8 / dt

Например, незатухающие колебания появились при kP 20, период колебаний составил 3 секунды. Период dt в системе будет 50 мс (0.05 с). Считаем:

• kP: 0.6*20=12
• kI: 12/3*2*0.05=0.4
• kD: 12*2/8/0.05=60

На полученных коэффициентах должны более-менее работать большинство систем, но не все. Также можно воспользоваться автоматическим тюнером коэффициентов, например два разных алгоритма встроены в библиотеку GyverPID.

Полезные страницы

• Набор GyverKIT – большой стартовый набор Arduino моей разработки, продаётся в России
• Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с AliExpress у проверенных продавцов
• Подборка библиотек для Arduino, самых интересных и полезных, официальных и не очень
• Полная документация по языку Ардуино, все встроенные функции и макросы, все доступные типы данных
• Сборник полезных алгоритмов для написания скетчей: структура кода, таймеры, фильтры, парсинг данных
• Видео уроки по программированию Arduino с канала “Заметки Ардуинщика” – одни из самых подробных в рунете
• Поддержать автора за работу над уроками
•  – сообщить об ошибке в уроке или предложить дополнение по тексту ()

Частотник danfoss vlt micro fc 51. Проблемы с установками частоты.

У меня возникла следующая проблема. Купили вытяжную приточную установку вместе со щитом управления. К щиту управления подключаются преобразователи частоты VLT Micro Drive – Danfoss, на вытяжную вентиляцию и на приток.

Не знаю как разобраться в описании: как настраивать преобразователь частоты, чтобы он мог выключаться командой с управляющего пульта. Частотный преобразователь работает один. Подключили к нему сеть питания – он работает. Отключать его можно, выключив автоматический выключатель или нажав кнопку на корпусе прибора. Это очень неудобно.

Я изучал инструкцию, очень большую, ответа так и не нашел на мой вопрос. Нашел лишь то, что написано: «сигнал управления подается на контакт №18. Взял и подключил на этот контакт сигнал управления, но ничего не изменилось.

Оказалось, что надо искать причину от того, что на частотный преобразователь не подключены контакты термореле от моторов вентиляторов. Это контролирование тока. Учитывая эту информацию, настроили частотный преобразователь VLT Micro Drive – Danfoss во 2-й раз. Есть электрическая схема, но в ней ничего не понятно.

Задача настройки

Настройка регулятора производится с одной единственной целью: подобрать его коэффициенты для данной задачи таким образом, чтобы регулятор поддерживал величину физического параметра на заданном уровне. В нашем примере физическая величина — это температура.

Допустим текущая температура в помещении 10 °С, а мы хотим, чтобы было 25°С. Мы включаем регулятор и он начинает управлять мощностью обогревателя таким образом, чтобы температура достигла требуемого уровня. Посмотрим как это может выглядеть.

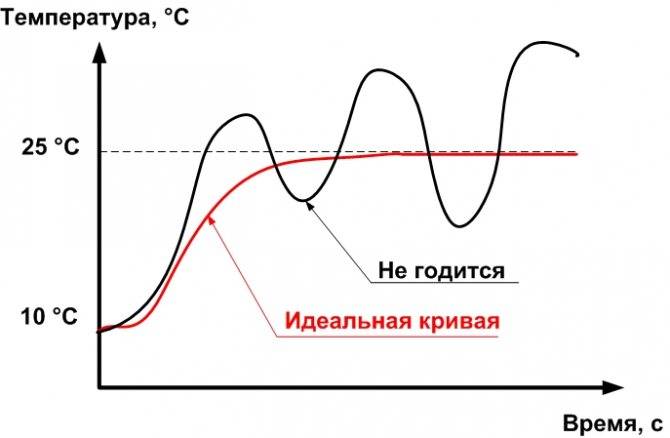
На данном рисунке красным цветом показана идеальная кривая изменения температуры в помещении при работе регулятора. Физическая величина плавно, без скачков, но в тоже время достаточно быстро подходит к заданному значению. Оптимальное время, за которое температура может достигнуть заданной отметки, определить довольно сложно. Оно зависит от многих параметров: размеров комнаты, мощности обогревателя и др. В теории это время можно рассчитать, но на практике чаще всего это определяется экспериментально.

Чёрным цветом показан график изменения температуры в том случае, если коэффициенты подобраны совсем плохо. Система теряет устойчивость. Регулятор при этом идёт «в разнос» и температура «уходит» от заданного значения.

Рассмотрим более благоприятные случаи.

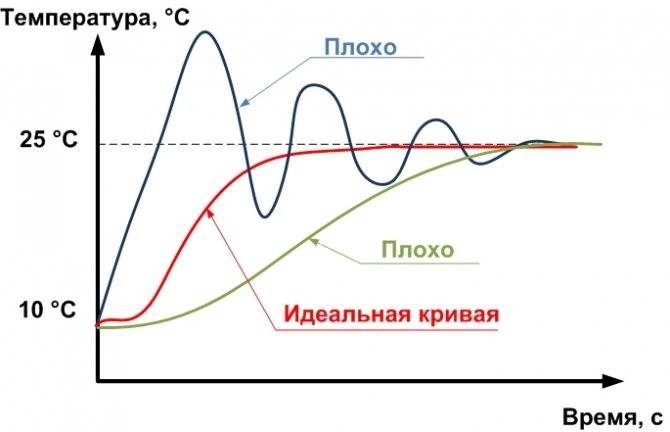
На этом рисунке показаны графики, далёкие от идеального. В первом случае наблюдается сильное перерегулирование: температура слишком долго «скачет» относительно уставки, прежде чем достичь её. Во втором случае регулирование происходит плавно, но слишком медленно.

А вот и приемлемые кривые:

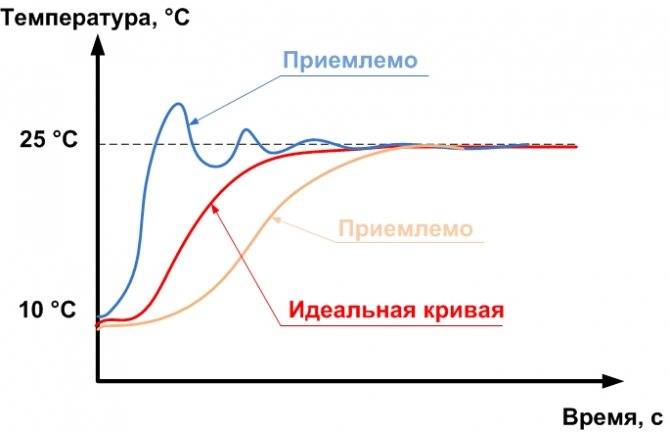
Данные кривые тоже не идеальны, но могут быть сочтены за удовлетворительные.

В процессе настройки регулятора, пользователю необходимо стремиться получить кривую, близкую к идеальной. Однако, в реальных условиях сделать это не так-то просто — приходится долго и мучительно подбирать коэффициенты. Поэтому зачастую останавливаются на «приемлемой» кривой регулирования. Например, в нашем примере нас могли бы устроить коэффициенты регулятора, при которых заданная температура достигалась бы за 15-20 минут с максимальным перерегулированием (максимальными «скачками» температуры) 2 °С. А вот время достижение уставки более часа и максимальные «скачки» температуры 5 °С — нас бы не устроили.

Далее поговорим о том, как подобрать коэффициенты для достижения оптимального регулирования. Рекомендуется настраивать коэффициенты в том же порядке, в котором это описано.

5.2.2. И-регулятор

Рассмотрим теперь случай, когда в ПИД-регуляторе остается только интегральный член, т.е. и . Из (5.39) получим

.

(5.47)

Модуль и аргумент передаточной функции (5.47) равны

, .

(5.48)

АЧХ И-регулятора в логарифмическом масштабе представляет собой прямую линию с наклоном ‑20дб/дек во всем диапазоне частот, от 0 до , которая пересекает ось частот (проведенную при ) в точке . ФЧХ представляет собой горизонтальную линию с ординатой .

На низких частотах, при , коэффициент передачи регулятора (5.48) больше единицы и стремится к бесконечности при . Поскольку случаю во временной области соответствует , или установившийся (равновесный) режим для асимптотически устойчивых систем, то передаточная функция любого устойчивого объекта (за исключением объектов с интегрирующими процессами, см. раздел ) при будет равна статическому коэффициенту передачи . Поэтому, подставляя в (5.42) и , получим для системы с И-регулятором

.

(5.49)

Рис. 5.38. Реакция на скачок замкнутой системы с объектом 2-го порядка (5.50) с И-регулятором при и разных

Это означает, что система с И-регулятором не имеет ошибки в установившемся режиме.

Отметим аналогию между И-регулятором и операционным усилителем. Операционный усилитель (ОУ) имеет передаточную функцию вида , параметры которой для типовых микросхем ОУ равны , . Поэтому практически во всем рабочем диапазоне частот и передаточная функция ОУ описывается упрощенным выражением , т.е. совпадает с передаточной функцией И-регулятора. Схемы включения ОУ также подобны структурам систем управления с И-регулятором.

На показаны переходные характеристики замкнутой системы с И-регулятором и объектом второго порядка вида

, где .

(5.50)

При больших постоянных интегрирования переходная характеристика имеет вид, сходный с характеристикой апериодического звена. С уменьшением растет усиление регулятора в соответствии с (5.48) и когда на частоте петлевое усиление контура с обратной связью приближается к 1, в системе появляются колебания (, кривая ).

Вторым фактором, влияющим на устойчивость замкнутой системы, является дополнительный сдвиг фаз величиной -, вносимый И-регулятором в контур регулирования. Поэтому объект 1‑го порядка с малой транспортной задержкой, или объект 2-го порядка, устойчивый в контуре с П-регулятором, может потерять устойчивость в контуре с И-регулятором.

Формула ПИД-регулятора

Как я и обещал, формул тут не будет… ну, почти не будет. И этот раздел – как раз и будет формулой. Обещаю – больше формул не будет! Так что потерпите!
Итак, формула ПИД-регулятора:
(навеяно Википедией)
Тут у нас следующие буковки (разъясним чуть ниже):

• u (t) — наша Функция;
• P — пропорциональная составляющая;
• I — интегральная составляющая;
• D — дифференциальная составляющая;
• e (t) – текущая ошибка;
• Kp — пропорциональный коэффициент;
• Ki — интегральный коэффициент;
• Kd — дифференциальный коэффициент;

Все, расслабились – больше эта формула нам в работе не понадобится, она для пояснения сути.
А суть тут такая.
У нас есть воздействие, наша Функция (u (t) ). Она состоит из трех составляющих – Пропорциональной, Интегральной и Дифференциальной (отсюда и ПИД-регулятор).
Формула в вышеприведенном виде хороша для изучения, но неудобна для расчетов (хотя бы потому, что в вычислительной технике надо переходить к численным методам). В программной реализации, если верить этой статье, переходят к дискретной реализации:
u(t) = P (t) + I (t) + D (t);
P (t) = Kp * e (t);
I (t) = I (t — 1) + Ki * e (t);
D (t) = Kd * {e (t) — e (t — 1)};
Вот это уже выглядит куда реальнее и понятнее! Мы вычисляем сумму трех составляющих. Каждая из них определяется своими коэффициентами. Если данный коэффициент нулевой, то составляющая в вычислении не участвует. С этой формулой мы и будем работать далее, ее я и реализую.
Впрочем, есть еще и другая, рекуррентная реализация:
u(t) = u(t — 1) + P (t) + I (t) + D (t);
P (t) = Kp * {e (t) — e (t — 1)};
I (t) = I * e (t);
D (t) = Kd * {e (t) — 2 * e (t — 1) + e (t — 2)};
Какая из них лучше/правильней? Математика, в общем-то, одинаковая. Коэффициенты тоже

Говорят, что есть разные подводные булыжники при реализации.
Обратите внимание! Коэффициенты тут – обязательно дробные числа! В языке программирования Си – как минимум float, а лучше бы и double.
Вся магия ПИД-регуляторов – именно в этих коэффициентах. Как их подбирать – посмотрим в конце

А сейчас переведем дух от математики и поедем к изучению поведения этой формулы.
Все расчеты и моделирование я проводил на модели в Excel. Он – файл – приложен внизу, с ним можно поиграться самостоятельно. Модель – сугубо для ознакомления с идеей! Т. е. не надо ее стараться привести к какому-то реальному процессу, искать в ней научный смысл и т. п. Там все цифры слегка «отфонарные». Но зато и файл простенький и несложный. И моделируется быстро. И дает возможность понять суть ПИД-регулятора. Пару слов по файлу я дам в конце.

Настройки ПИД-регулятора

Наладка ПИД-регулятора сводится к определению коэффициентов Kp, Ki, Kd. Компоненты определяются из формулы:

По ним определяются передаточные функции системы автоматического регулирования и вычисляются ее параметры:

• Точность.
• Скорость регулирования.
• Форма графиков переходных процессов.
• Инерционность.
• Другие величины и функции.

Математическая модель САР не может дать полного представления о работе системы. Расчеты выполняются для «идеального регулятора». Нелинейность контролируемых параметров, внешние возмущения, помехи на объекте управления не позволяют применять данные расчетов для построения системы автоматического регулирования на практике. Результаты математических расчетов используют как вспомогательные данные.

При разработке ПИД-регуляторов и САР используют оборудование, имитирующее изменение контролируемых характеристик, измерительные приборы и ПК. Устройства позволяют определить и анализировать реакцию системы на воздействия и более точно подобрать коэффициенты.

На практике применяется опытный подбор коэффициентов. ПИД-регуляторы устанавливают на объекте, вводят коэффициенты, полученные при расчете или стендовых испытаниях, настраивают параметры на месте.

5.2.3. ПИ-регулятор

В ПИ-регуляторе только постоянная дифференцирования равна нулю, :

.

(5.51)

Рис. 5.39. Реакция замкнутой системы с ПИ регулятором на скачок при для объекта вида (5.50) при	Рис. 5.40. Реакция замкнутой системы с ПИ регулятором на скачок при для объекта вида (5.50) при

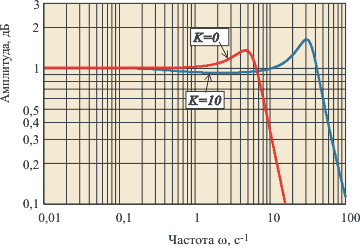
АЧХ ПИ-регулятора можно получить из , если отбросить правую ветвь АЧХ с наклоном +20 дБ/дек. При этом сдвиг фаз на частотах выше 1 Гц (на ) не превысит уровень 0˚. Таким образом, ПИ-регулятор имеет два существенных положительных отличия от И-регулятора: во-первых, его усиление на всех частотах не может стать меньше , следовательно, увеличивается динамическая точность регулирования, во-вторых, по сравнению с И-регулятором, он вносит дополнительный сдвиг фаз только в области низких частот, что увеличивает запас устойчивости замкнутой системы. Оба фактора дают дополнительные степени свободы для оптимизации качества регулирования. В то же время, как и в И-регуляторе, модуль коэффициента передачи регулятора с уменьшением частоты стремится к бесконечности, обеспечивая тем самым нулевую ошибку в установившемся режиме. Отсутствие сдвига фаз на высоких частотах позволяет увеличить скорость нарастания управляемой переменной (по сравнению с И-регулятором) без снижения запаса устойчивости. Однако это справедливо до тех пор, пока пропорциональный коэффициент не станет настолько большой, что увеличит усиление контура до единицы на частоте .

Переходный процесс в ПИ-регуляторе при разных сочетаниях и показан на , . При () получаем И-регулятор. С ростом пропорционального коэффициента появляется дополнительная ошибка во время переходного процесса (см. также и (5.45)), которая уменьшается с ростом , однако при этом снижается запас устойчивости системы, поскольку с ростом увеличивается усиление на частоте . Это приводит к появлению затухающих колебаний в начале переходного процесса (). Когда величина становится достаточно большой для компенсации ослабления сигнала в объекте на частоте , в системе появляются незатухающие колебания.

Следует отметить, что в отличие от П-регулятора, в котором ошибка остается в установившемся режиме, наличие интегрального члена в ПИ-регуляторе сводит эту ошибку в идеальном регуляторе до нуля, как в И-регуляторе. Выражение для ошибки ПИ-регулятора можно получить, подставив (5.51) в (5.41) и вычтя из полученного выражения :

.

(5.52)

Рис. 5.41. АЧХ замкнутого контура с ПИ-регулятором при для объекта вида (5.50) при

Как видим, при , т.е. в установившемся режиме, ошибка .

Однако появление пропорционального коэффициента приводит к затягиванию переходного процесса по сравнению с И-регулятором при тех же и , (). Объясняется это тем, что в ПИ-регуляторе сигнал ошибки , поступающий на вход интегратора, меньше, чем в И-регуляторе (он уменьшается благодаря пропорциональному коэффициенту), поэтому сигнал, компенсирующий ошибку нарастает медленнее, чем в И-регуляторе. В частотной области этот процесс можно объяснить тем, что с ростом полюс передаточной функции смещается влево (), т.е. расширяется область частот, в которой интегральной составляющая пренебрежимо мала и ПИ-регулятор вырождается в чистый П-регулятор, для которого характерна статическая ошибка. В АЧХ замкнутой системы с большим () появляется погрешность (уменьшение амплитуды выходного сигнала) в диапазоне частот выше . С ростом эта частота сдвигается влево, что во временной области соответствует затягиванию процесса установления.

Работа регулятора в обратном и прямом действии

Множество регуляторов имеют принцип прямого действия. Повышение скорости двигателя приводит к повышению переменной величины процесса. Это случай в системе насосов, давление это величина переменная процесса. Повышение скорости двигателя обуславливает повышение давления. Во многих системах повышение скорости двигателя обуславливает к снижению параметра переменной процесса. Температура вещества, которое обдувается вентиляционной системой теплообменника – процессная переменная величина: при повышении скорости вентиляционной системы температура вещества снижается. В этом разе нужно применить регулятор действия обратного вида.

Синтез замкнутой системы и настройка регулятора

Состоящая из четырех рычагов модель механизма моделируется в SimMechanics, а двигатель постоянного тока моделируется в SimElectronics. Для создания архитектуры регулятора, показанной на рис. 2, следует добавить блок ПИД-регулятора с дискретизацией по времени из библиотеки Simulink Discrete. Теперь, когда система управления с обратной связью создана, можно перейти к настройке регулятора.

Для этого требуется открыть диалоговое окно блока PID Controller («ПИД-регулятор»), указать период дискретизации и нажать кнопку Tune («Настройка»). Откроется окно PID Tuner (рис. 3).

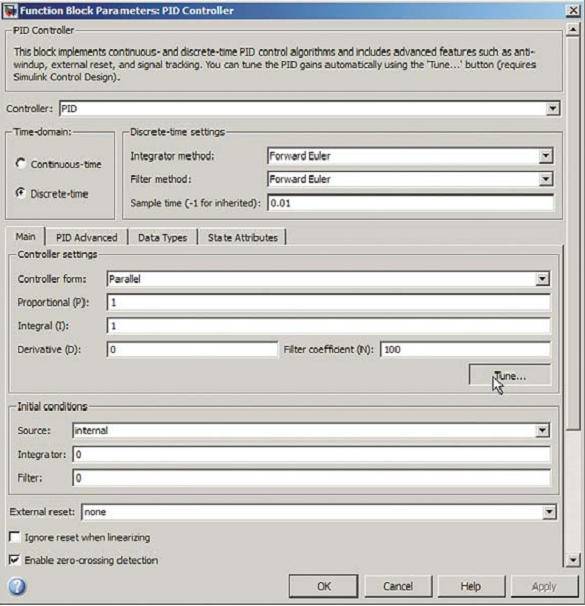
Рис. 3. Окно настройки PID Tuner, открытое с помощью диалогового окна блока

Интерфейс настройки Simulink Control Design линеаризует объект в текущей рабочей точке и строит линейную модель объекта с постоянными параметрами (LTI), с которой взаимодействует блок ПИД-регулятора в замкнутом контуре управления. Вычислительная задержка, связанная с дискретизацией сигнала, учитывается автоматически. Используя метод автоматической настройки, интерфейс Simulink Control Design вычисляет первоначальные коэффициенты усиления ПИД-регулятора. Этот метод не накладывает никаких ограничений на порядок объекта или постоянную времени, причем он работает в областях как непрерывного, так и дискретного времени.

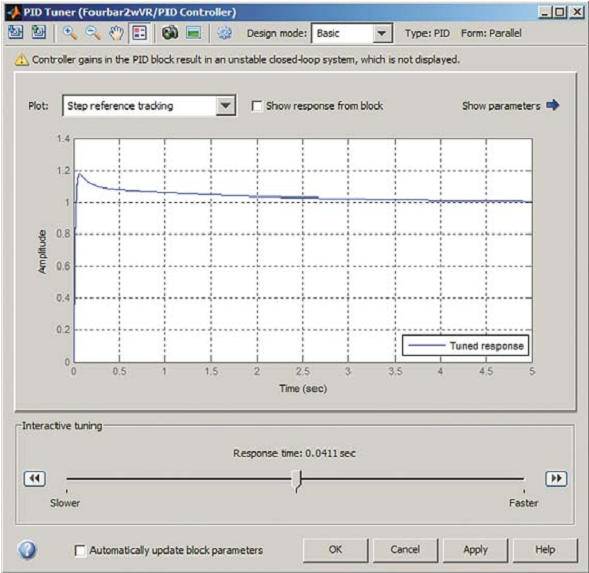
Рис. 4. Первоначальные параметры, рассчитанные PID Tuner

На рис. 4 показана реакция на ступенчатое воздействие в рабочей точке замкнутой системы с первоначальными коэффициентами ПИД-регулятора. Если регулятор работает удовлетворительно, следует нажать кнопку Apply («Применить»), чтобы обновить значения коэффициентов усиления P, I, D и N в диалоговом окне блока PID Controller («ПИД-регулятор»). Затем можно проверить работу системы, моделируя нелинейности и контролируя результаты (рис. 5). Также можно произвести настройку в интерактивном режиме с помощью ползунка, увеличивая или понижая быстродействие регулятора (рис. 4).

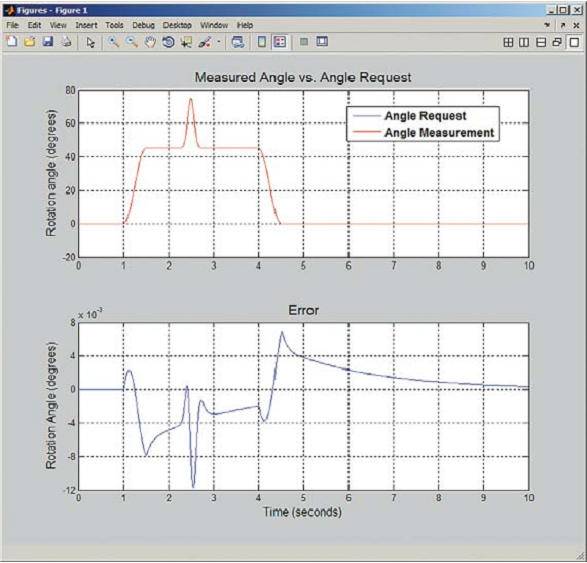
Рис. 5. Результаты моделирования модели четырехзвенного шарнирного механизма

5.2.1. П-регулятор

Пусть интегральная и дифференциальная компоненты отсутствуют, т.е. . Тогда из (5.40) получим и (5.42) можно преобразовать к виду

.

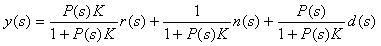(5.43)

В установившемся режиме, при или передаточная функция процесса равна коэффициенту передачи . При этом выражение (5.43) преобразуется к виду

.

(5.44)

Как следует из полученной формулы, влияние возмущений d  снижается с ростом петлевого усиления и при обратно пропорционально коэффициенту регулятора . Однако проблема устойчивости не позволяет выбирать как угодно большим.

Влияние помехи n также уменьшается с ростом петлевого усиления и пропорционального коэффициента регулятора. Дополнительно влияние помехи можно уменьшить применением экранирования, правильного заземления, витых пар, уменьшением длины проводников в цепи обратной связи и др., см. []).

При пренебрежимо малых помехах и внешних возмущениях погрешность П-регулятора , как следует из (5.44), определяется величиной пропорционального коэффициента усиления:

.

(5.45)

Эта погрешность обычно не может быть сделана как угодно малой путем увеличения усиления регулятора, поскольку с ростом сначала падает запас по фазе и усилению системы с обратной связью, что ухудшает ее робастность и качество регулирования, затем возникают периодические колебания (система теряет устойчивость), см. . Поэтому в П-регуляторах для снижения погрешности используют метод компенсации. Для этого к входу объекта регулирования прикладывают компенсирующее воздействие , которое аддитивно добавляется к возмущению d, чтобы суммарное воздействие возмущения и компенсирующего воздействия стало равно . Отметим, что при изменении значения уставки компенсацию нужно выполнить заново, поскольку погрешность (5.45) пропорциональна (т.е. является мультипликативной), а компенсация в виде является аддитивной (не зависит от ).

Скомпенсировать погрешность можно также с помощью коррекции величины . Для этого управляющее воздействие после коррекции (обозначим его ), как следует из (5.44) и (5.45), должно иметь вид

.

(5.46)

Рис. 5.37. Изменение переменной во времени при подаче единичного скачка на вход системы при разных

Переходный процесс в контуре с П-регулятором при и разных показан на . При малых система имеет малое перерегулирование, но большую статическую погрешность (50%). С ростом погрешность уменьшается, но возрастает перерегулирование.

Объясняется поведение П-регулятора следующим образом. С ростом усиления вся АЧХ разомкнутой системы (АЧХ петлевого усиления , ) сдвигается вверх, в том числе возрастает усиление на частоте , где фазовый сдвиг в контуре с обратной связью равен 180˚. Это приводит к уменьшению запаса по фазе и усилению, возрастает колебательность и перерегулирование. Если петлевое усиление на частоте достигает 1, в системе устанавливаются незатухающие колебания. Подробнее описание этого процесса см. в разделе