Законы отражения света и история их открытия

Явление обратного отражения

Феномен обратного отражения, или ретроотражения, заключается в способности некоторых поверхностей или объектов отражать падающий на них пучок света обратно к источнику, от которого он пришел, независимо от того, под каким углом на них падает этот свет.

Такое поведение можно наблюдать в случае плоского зеркала, но только тогда, когда световой пучок падает на него перпендикулярно, то есть угол падения равен 90°.

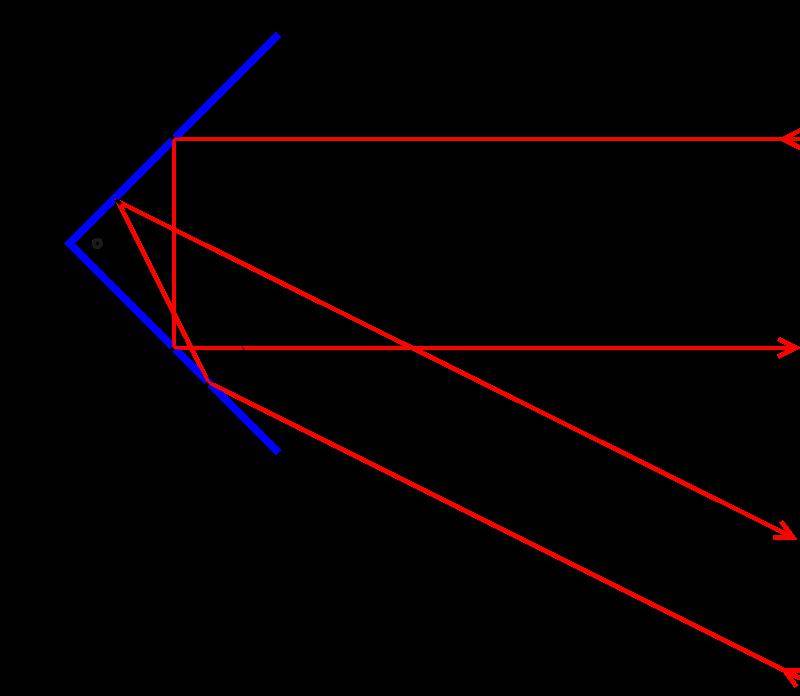
Простой ретрорефлектор можно изготовить, если соединить два зеркала перпендикулярно друг к другу. Изображение, которое дает такой прибор, всегда того же размера, что и оригинальное, но будет перевернутым

При этом не важно, под какими углами на этот ретрорефлектор падают световые лучи, он всегда их отражает на 180°. Ниже на рисунке приведен этот ретрорефлектор, и продемонстрированы его физические свойства

Законы – основа всего

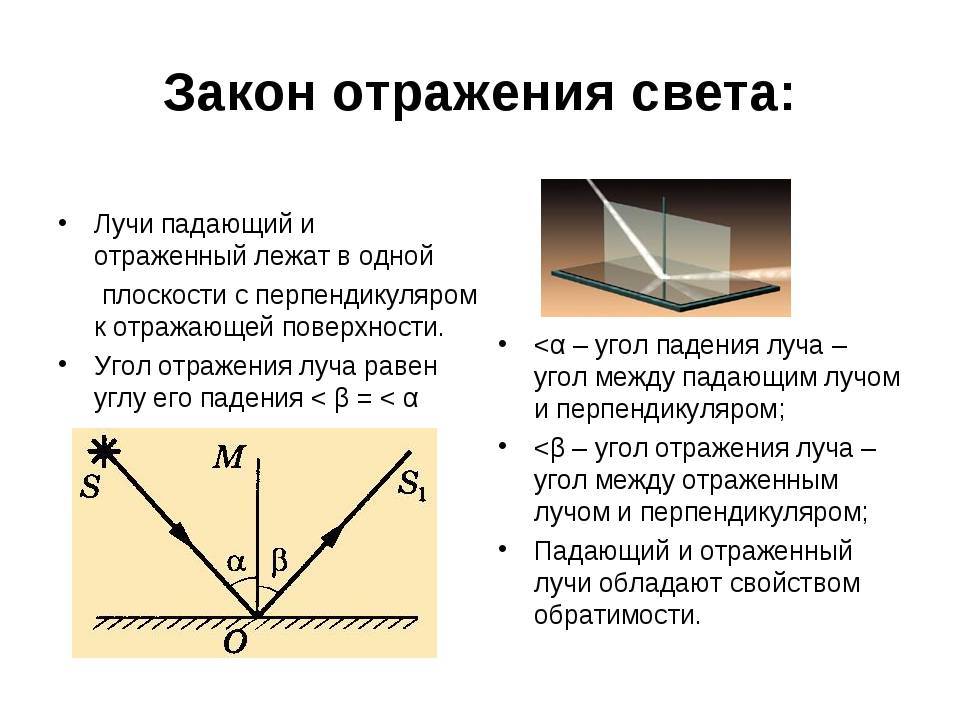
Закон отражения светового потока определяется как физическое явление, в ходе которого свет, направляющийся из одной среды в другую, на их разделе будет частично возвращен обратно.

Отражение света на границе раздела

Зрительный анализатор человека наблюдает свет в момент, когда луч, идущий от своего источника, попадает в глазное яблоко. В ситуации, когда тело не выступает в роли источника, зрительный анализатор может воспринимать лучи от иного источника, которые отражаются от тела. При этом световое излучение, падающее на поверхность объекта, может изменить направление своего дальнейшего распространения. В результате этого тело, которое отражает свет, будет выступать в роли его источника. При отражении часть потока будет возвращаться в первую среду, из которой он первоначально направлялся. Здесь тело, которое отразит его, станет источником уже отраженного потока.
Существует несколько законов для данного физического явления:

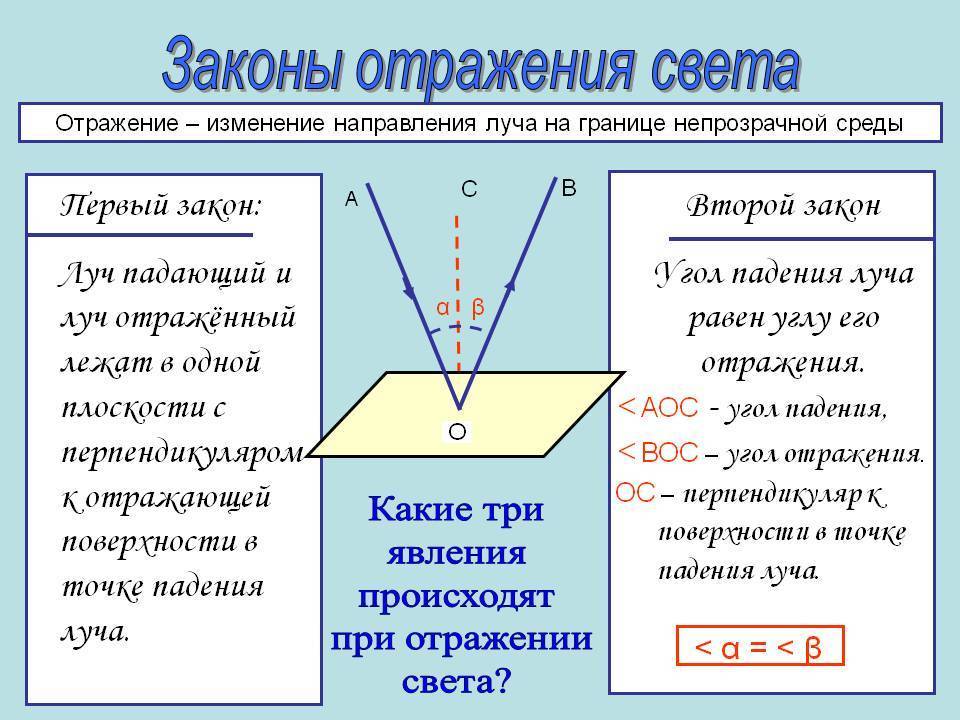
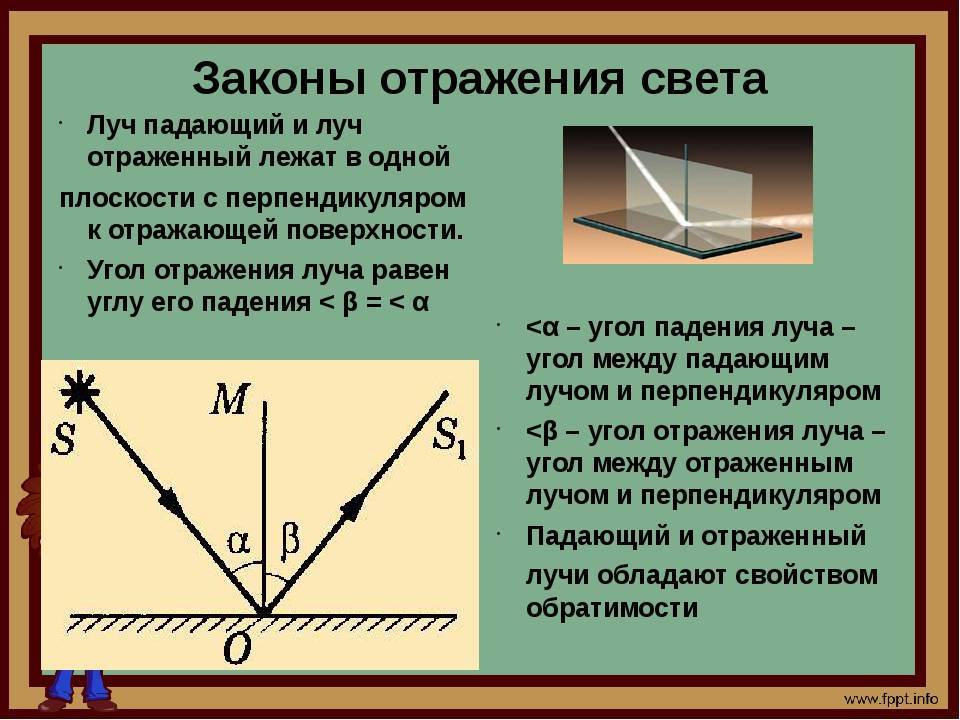
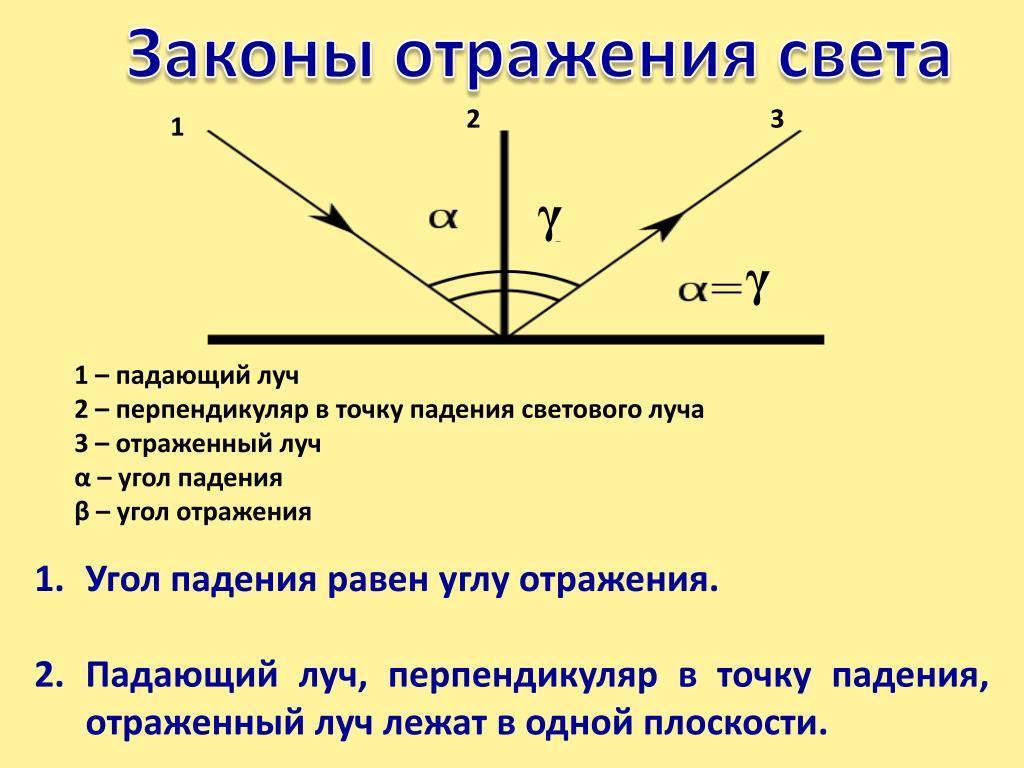
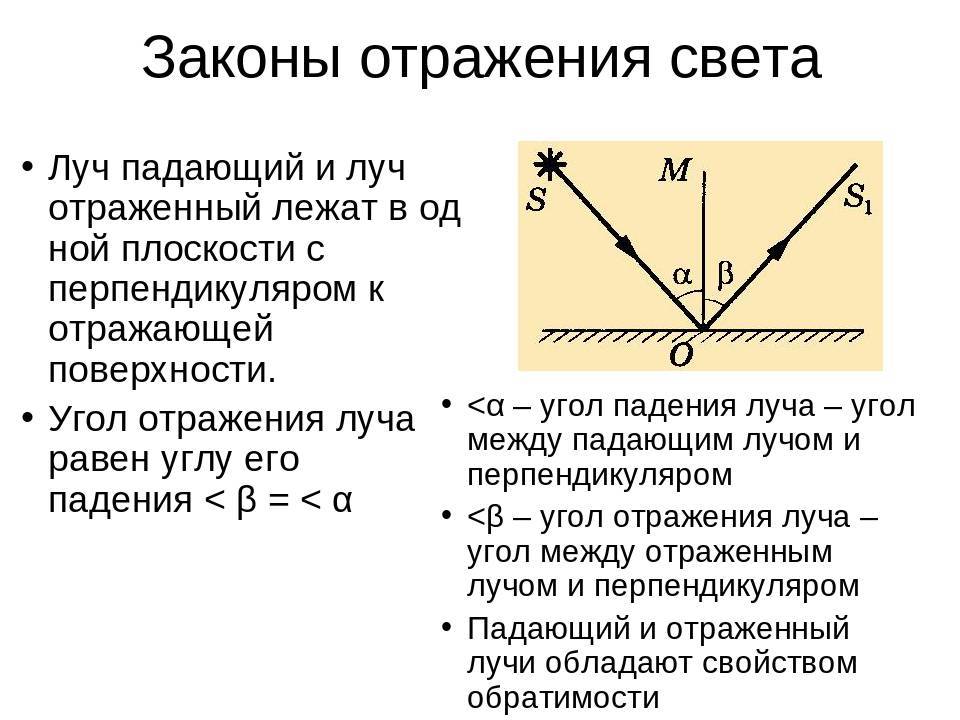
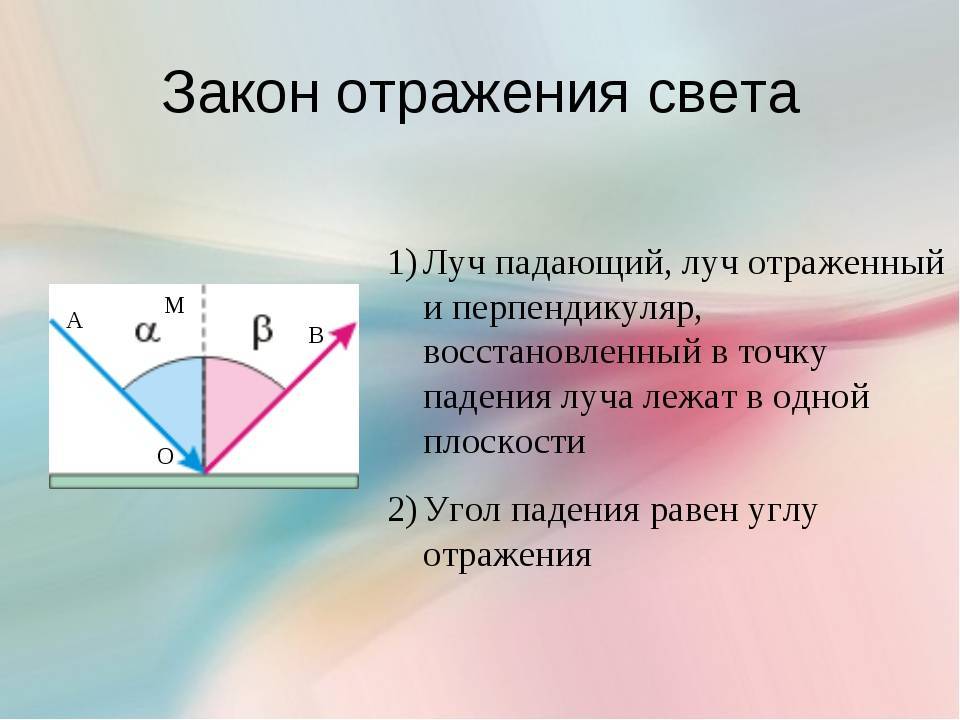
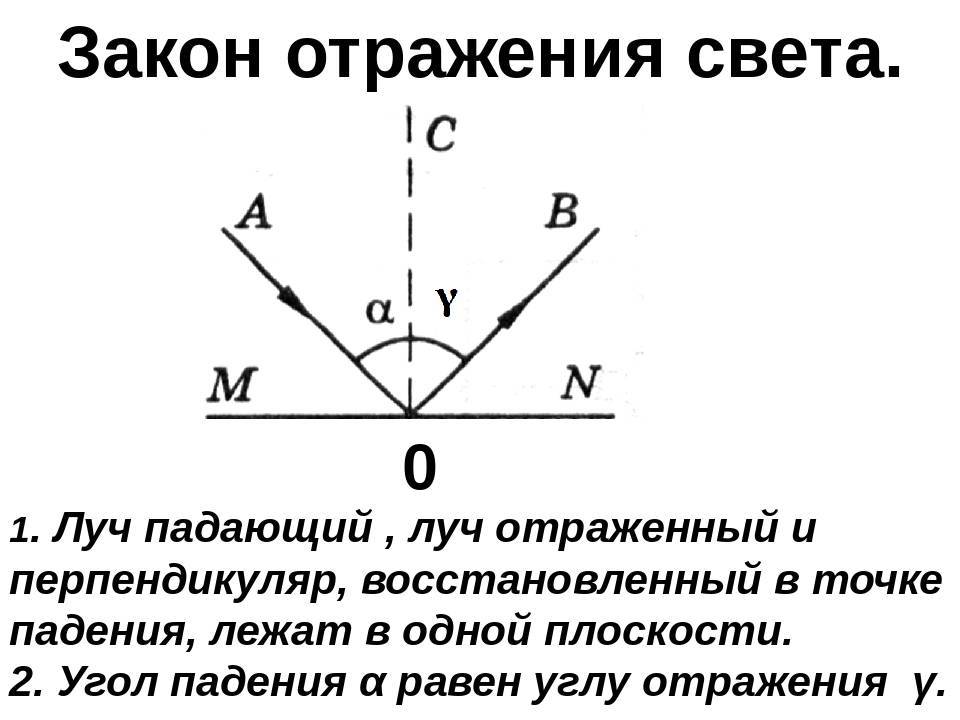
первый закон гласит: отражающий и падающий луч, вместе с перпендикулярной линией, возникающей на границе раздела сред, а также в восстановленной точке падения светового потока, должны располагаться в одной плоскости;

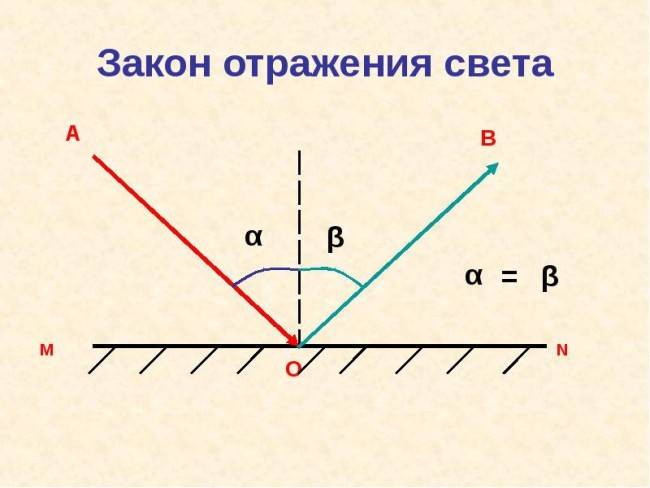
Первый и второй закон

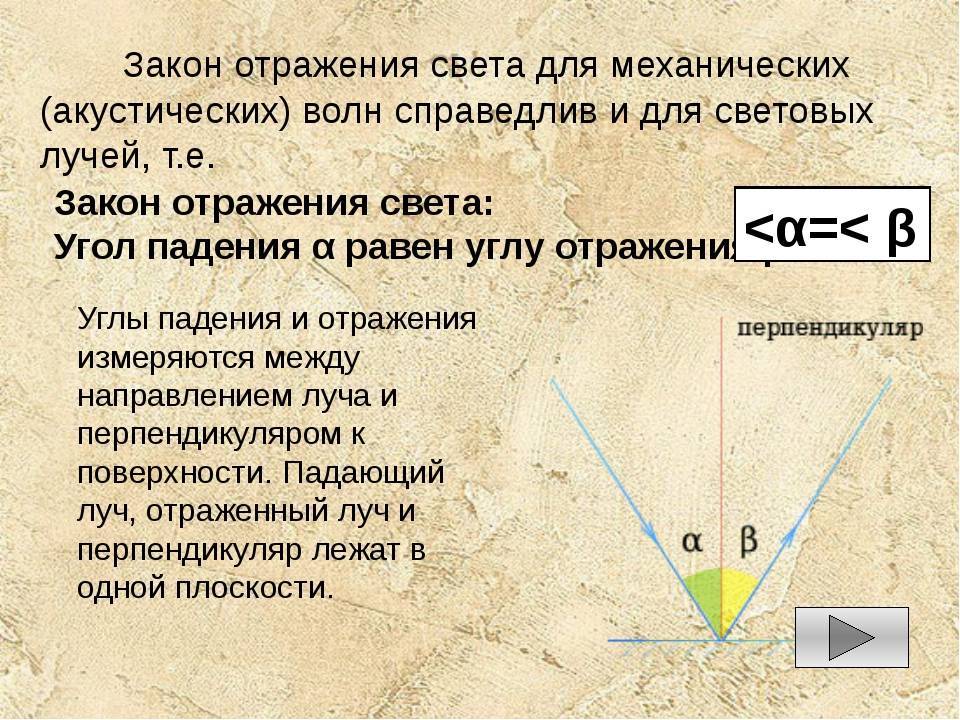
второй закон. Его формулировка имеет следующий вид: угол отражения светового потока будет равен углу падения. Это связано с тем, что они обладают взаимно перпендикулярными сторонами

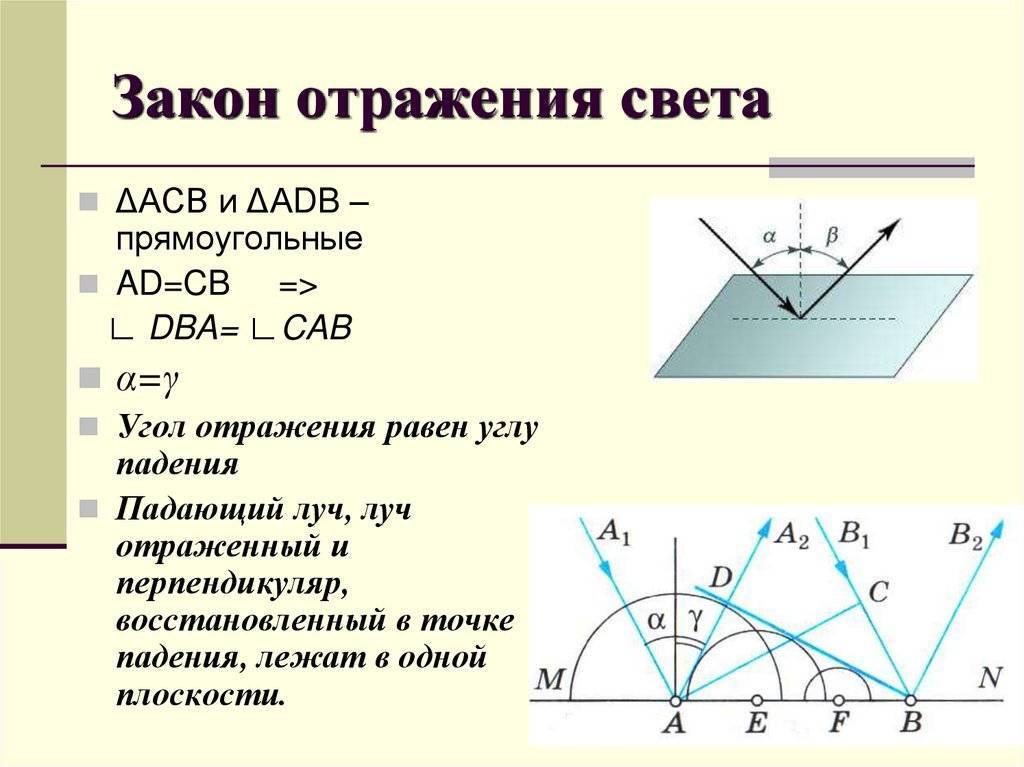
Беря во внимание принципы равенства треугольников, становится понятным, откуда берется это равенство. Используя данные принципы можно легко доказать то, что эти углы находятся в одной плоскости с проведенной перпендикулярной линией, которая была восстановлена на границе разделения двух веществ в точке падения светового луча

Эти два закона в оптической физике являются основными. При этом они справедливы и для луча, имеющего обратный ход. В результате обратимости энергии луча, поток, распространяющийся по пути ранее отраженного, будет отражаться аналогично пути падающего.

Принцип Гюйгенса. Закон отражения света

Подробности

Просмотров: 706

«Физика – 11 класс»

Законы отражения и преломления света можно вывести из одного общего принципа, описывающего поведение волн.
Этот принцип впервые был выдвинут современником Ньютона Христианом Гюйгенсом.

Принцип Гюйгенса

Согласно принципу Гюйгенса каждая точка волнового фронта является источником вторичных волн.
Для того чтобы, зная положение волновой поверхности (фронта волны) в момент времени t, найти ее положение в следующий момент времени t + Δt, нужно каждую точку фронта рассматривать как источник вторичных волн.
Точки M₁, М₂, М₃ и т. д. являются такими источниками.
Поверхность, касательная к фронтам вторичных волн, представляет собой фронт первичной волны в следующий момент времени.
Этот принцип в равной мере пригоден для описания распространения волн любой природы: механических, световых и т. д.
Гюйгенс сформулировал его первоначально именно для световых волн.

Для механических волн принцип Гюйгенса имеет наглядное истолкование: частицы среды, до которых доходят колебания, в свою очередь, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют.

Закон отражения

С помощью принципа Гюйгенса можно вывести закон, на основе которого объясняется отражение волн от границы раздела сред.

Рассмотрим, как происходит отражение плоской волны.
Волна называется плоской, если поверхности равной фазы (волновые поверхности) и соответственно фронт волны представляют собой плоскости.
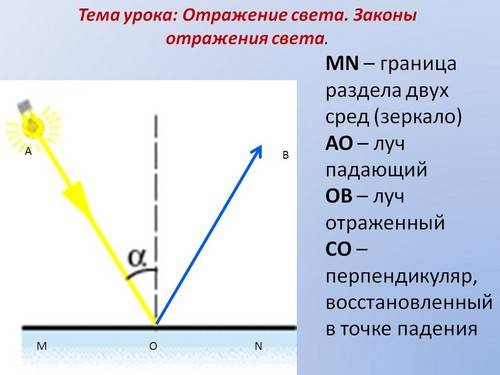
На рисунке MN — отражающая поверхность; прямые А₁А и В₁В — два луча падающей плоской волны.
Плоскость АС — фронт волны в момент времени, когда луч А₁А дошел до отражающей поверхности.

Угол α между падающим лучом и нормалью к отражающей поверхности в точке падения называют углом падения.

Волновую поверхность отраженной волны можно получить, если провести огибающую вторичных волн, центры которых лежат на границе раздела двух сред.
Различные участки волновой поверхности АС достигают отражающей границы не одновременно.
Возбуждение колебаний в точке А начнется раньше, чем в точке В, на время (υ — скорость волны).

В момент, когда волна достигнет точки В и в этой точке начнется возбуждение колебаний, вторичная волна с центром в точке А уже будет представлять собой полусферу радиусом r = AD = υΔt = СВ.
Фронты вторичных волн от источников, расположенных между точками А и В, показаны на рисунке.
Огибающей фронтов вторичных волн является плоскость DB, касательная к сферическим поверхностям.
Она и представляет собой фронт отраженной волны.
Лучи АА₂ и ВВ₂ перпендикулярны фронту отраженной волны DB.
Угол у между нормалью к отражающей поверхности и отраженным лучом называют углом отражения.

Так как AD = СВ и треугольники ADB и АСВ прямоугольные, то ∠DBA = ∠CAB.
Но α = ∠CAB и γ = ∠DBA как углы с взаимно перпендикулярными сторонами.
Следовательно, угол отражения равен углу падения

α = γ

Здесь и далее в алгебраических соотношениях под словом угол подразумевается его радианная (или градусная) мера

Из теории Гюйгенса вытекает закон отражения света: луч падающий, луч отраженный и нормаль к отражающей поверхности в точке падения лежат в одной плоскости, причем угол падения равен углу отражения.

При обратном направлении распространения световых лучей отраженный луч станет падающим, а падающий — отраженным

Обратимость хода световых лучей — их важное свойство

Сформулирован общий принцип распространения волн любой природы — принцип Гюйгенса.
Этот принцип позволяет с помощью простых геометрических построений находить волновую поверхность в любой момент времени по известной волновой поверхности в предшествующий момент.
Из принципа Гюйгенса выведен закон отражения света.

Следующая страница «Закон преломления света»

Назад в раздел «Физика – 11 класс, учебник Мякишев, Буховцев, Чаругин»

Световые волны. Физика, учебник для 11 класса – Класс!ная физика

Оптика —
Скорость света —
Принцип Гюйгенса. Закон отражения света —
Закон преломления света —
Полное отражение —
Линза —
Построение изображения в линзе —
Формула тонкой линзы. Увеличение линзы —
Примеры решения задач. Геометрическая оптика —
Дисперсия света —
Интерференция механических волн —
Интерференция света —
Некоторые применения интерференции —
Дифракция механических волн —
Дифракция света —
Дифракционная решетка —
Поперечность световых волн. Поляризация света —
Поперечность световых волн и электромагнитная теория света —
Примеры решения задач. Волновая оптика —
Краткие итоги главы

Как проходит свет в разных средах?

Различные среды преломляют лучи по-разному. Так, на границе между воздухом и водой угол преломления примерно 30о, а на границе воздух – алмаз, угол преломления около 21о. Причем, это с одним углом падения в 60о.

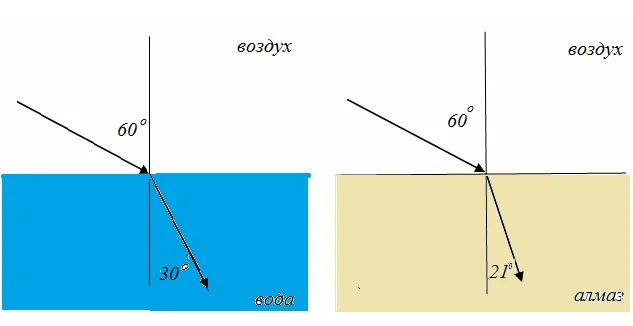
Не всегда угол преломления меньше угла падения, как в приведенных примерах. Если вспомнить, что свет – это электромагнитная волна, то значит, он обладает скоростью (300 000 км/с в вакууме). В веществах скорость света другая, всегда меньше.

На своем пути лучи света проходят по различным прозрачным веществам, которые образуют оптическую среду. Если скорость света в одной среде больше, чем в другой, то первая среда называется оптически менее плотной, а вторая – оптически более плотной средой. Например, попадая в воду из воздуха, лучи света переходят из оптически менее плотной среды (воздух) в оптически более плотную (воду).

Преломление лучей на границе раздела связано с оптической плотностью каждой из сред следующим правилом:

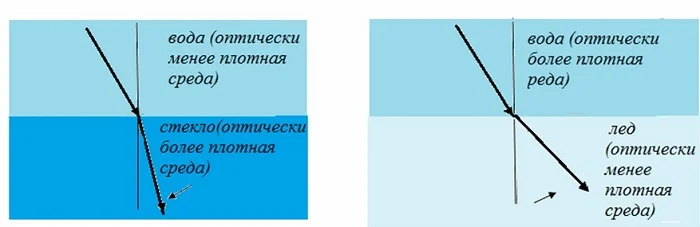
Отсюда видно, что угол преломления может быть больше или меньше угла падения. Все объясняется оптическими свойствами среды, куда переходит световой луч.

Построение изображений в плоском зеркале

Построение изображения в плоском зеркале основано на законах отражения света.

Алгоритм построения изображения в плоском зеркале

1. Проведите из данной точки на поверхность луч под произвольным углом. В точке падения луча на границу раздела сред проведите перпендикуляр.
2. Отметьте угол падения ​\( \alpha \)​.
3. Постройте равный ему угол отражения ​\( \beta \)​.
4. Проведите из данной точки перпендикуляр к поверхности зеркала ​\( (\alpha=0) \)​.
5. Постройте равный ему угол отражения ​\( (\beta=0) \)​ (эти лучи совпадают).
6. Проведите пунктирной линией продолжения отраженных лучей за зеркало.
7. Найдите точку пересечения продолжений отраженных лучей (эта точка является изображением данной точки в плоском зеркале).
8. Аналогично постройте изображение второй точки.
9. Соедините полученные изображения точек пунктирной линией.

Изображение предмета в плоском зеркале мнимое, прямое, по размерам равное предмету, находящееся за зеркалом на таком же расстоянии, на каком предмет находится перед зеркалом.

Важно!
Если на поверхность плоского зеркала падает сходящийся пучок лучей, то изображение получается действительным

Если поверхность двух плоских зеркал образует угол ​\( \varphi \)​, то количество изображений в такой системе зеркал можно определить по формуле:

где ​\( N \)​ – количество изображений.

Почему сломался карандаш?

Наблюдательный рыболов видит, что весла от его лодки при погружении в воду как будто ломаются. Когда весла над поверхностью воды, они снова прямые. Почему? Это объясняют оптические законы.

Взмахнуть рукой в воздухе гораздо легче, чем провести рукой внутри воды. Вот и свет проходит в разных средах (например, в вакууме, стекле, воздухе, алмазе, воде) тоже по-разному. На границе двух различных сред меняется направление хода лучей света.

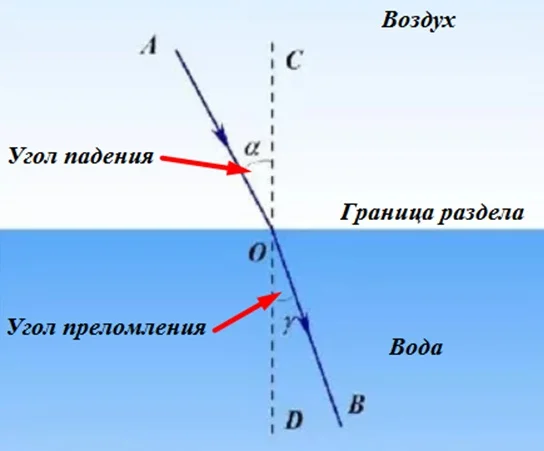
Углы падения и преломления, которые определяются, как и при отражении, с помощью перпендикуляра к границе раздела, в данном случае не равны. 

 

Вот почему карандаш выглядит в стакане сломанным. Здесь не нужно путать световые лучи и сам карандаш. Лучи идут человеку в глаз, как показано на чертеже. То, что карандаш воспринимается глазом в сломанном виде – это оптическая иллюзия, созданная ходом всех лучей, отражающихся от карандаша.

Мы видим предметы за счет отражения света

С явлением отражения света мы сталкиваемся ежедневно. Наше утро начинается с умывания перед зеркалом, в котором мы видим свое отражение. Свет отражается в окнах домов, витринах магазинов, в автомобильных зеркалах и т.д.

Отражаясь от поверхностей предметов, свет попадает в глаз человека, формирует изображение на сетчатке глаза и, тем самым, позволяет нам видеть окружающий мир. В ночное время солнечный свет отсутствует, поэтому разглядеть предметы можно только, если они сами излучают свет (например, фонари, окна домов), либо, если мы сами воспользуемся внешней подсветкой (фонариком, прожектором).

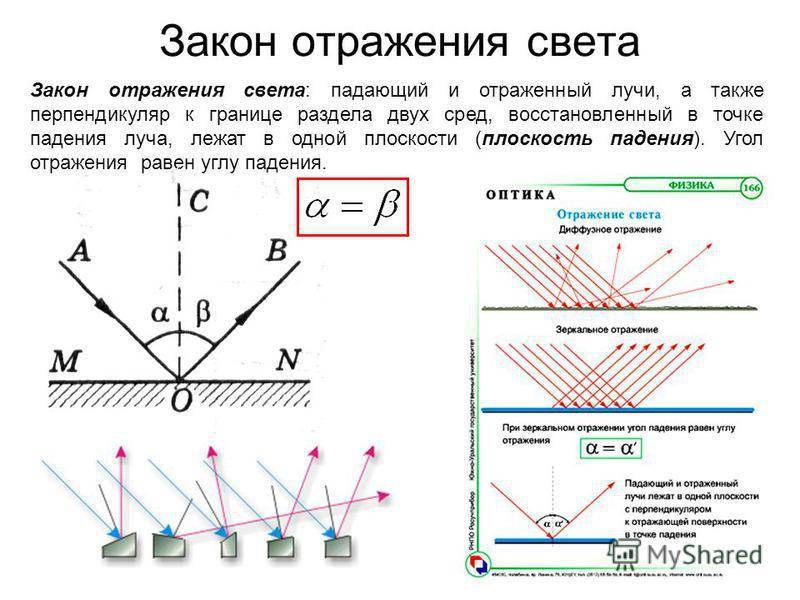
Рис. 1. Примеры отражения света. Зеркальное и диффузное отражения.

В зависимости от качества границы раздела различают зеркальное и диффузное отражения. Зеркальным называется отражение от очень гладких поверхностей, которые еще называют оптически гладкими, когда величина неровностей поверхности меньше 1 мкм. Лучи света при этом отражаются в одном направлении.

Диффузное отражение света происходит от шероховатых (матовых) поверхностей. Отражение лучей света происходит в разных направлениях. Когда часть поверхности зеркальная, а часть матовая, то в таком случае говорят о смешанном отражении.

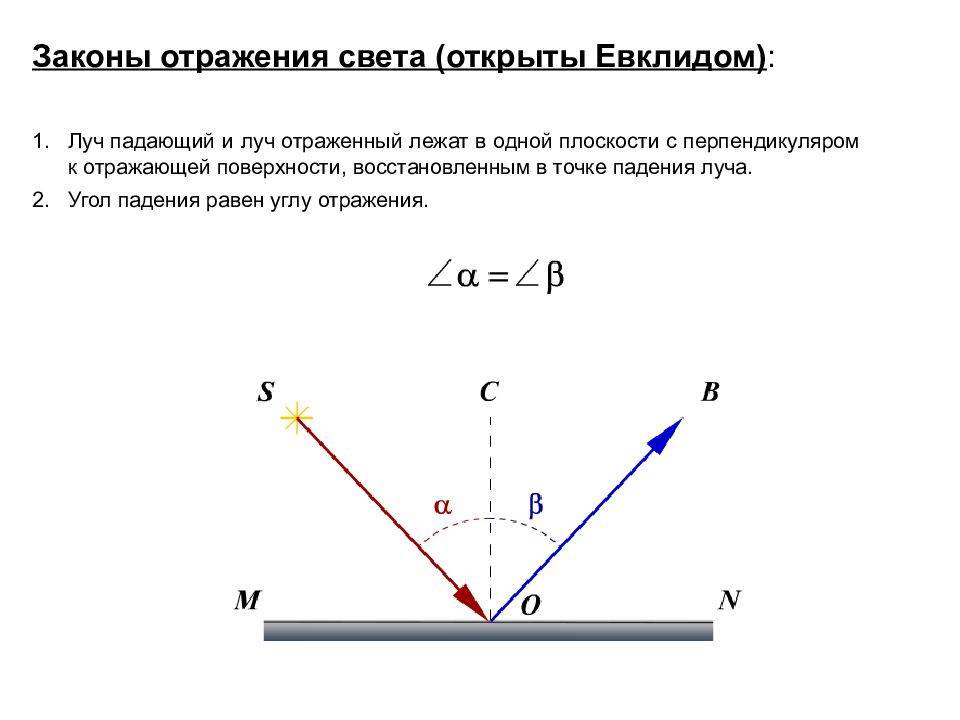
Первые попытки сформулировать закономерности отражения света найдены в трактате “Катоптрика” знаменитого древнегреческого математика Эвклида, написанного им примерно в 300 г. до н. э.

Геометрическая оптика. Основные законы геометрической оптики

Задолго до возникновения понимания истинной физической природы света человечеству уже были известны основные законы геометрической оптики.

Закон прямолинейного распространения света

Определение 1

Закон прямолинейного распространения света гласит, что в оптически однородной среде свет распространяется прямолинейно.

Подтверждением этому служат резкие тени, которые отбрасываются непрозрачными телами при освещении с помощью источника света сравнительно малых размеров, то есть так называемым «точечным источником».

Иное доказательство заключается в достаточно известном эксперименте по прохождению света далекого источника сквозь малое отверстие, с образующимся в результате узким световым пучком. Данный опыт подводит нас к представлению светового луча в виде геометрической линии, вдоль которой распространяется свет.

Определение 2

Стоит отметить тот факт, что само понятие светового луча вместе с законом прямолинейного распространения света утрачивают весь свой смысл, в случае если свет проходит через отверстия, размеры которых аналогичны с длиной волны.

Исходя из этого, геометрическая оптика, которая опирается на определение световых лучей – это предельный случай волновой оптики при λ→, рамки применения которой рассмотрим в разделе, посвященном дифракции света.

На грани раздела двух прозрачных сред свет может частично отразиться таким образом, что некоторая часть световой энергии будет рассеиваться после отражения по уже новому направлению, а другая пересечет границу и продолжит свое распространение во второй среде.

Закон отражения света

Определение 3

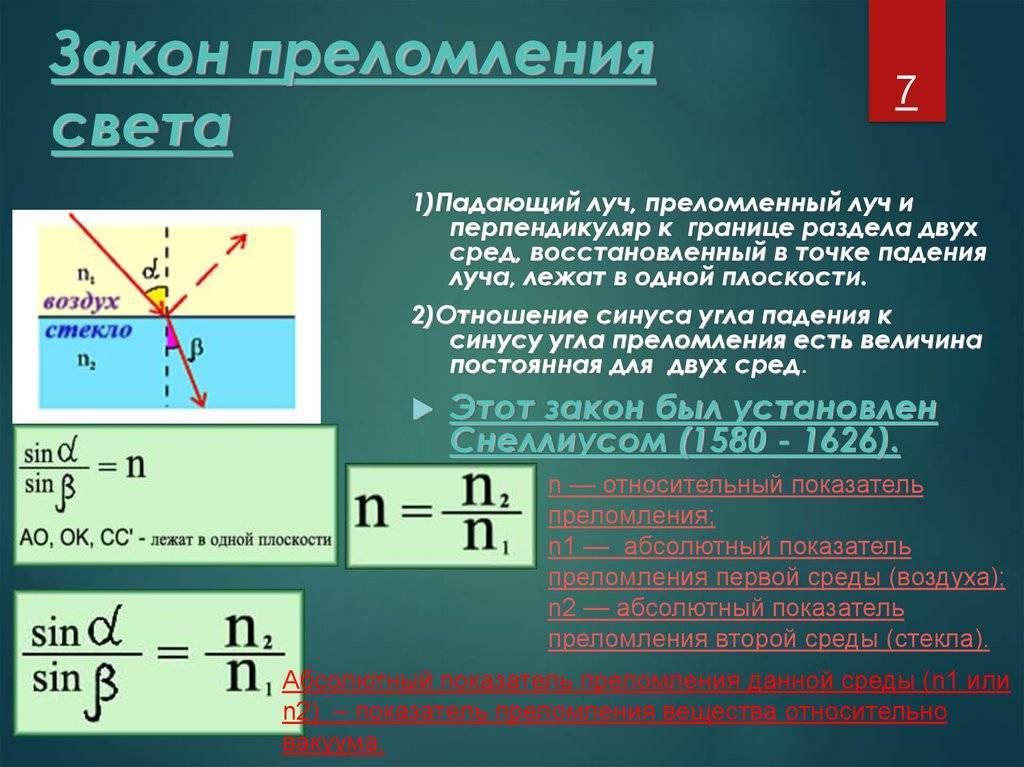
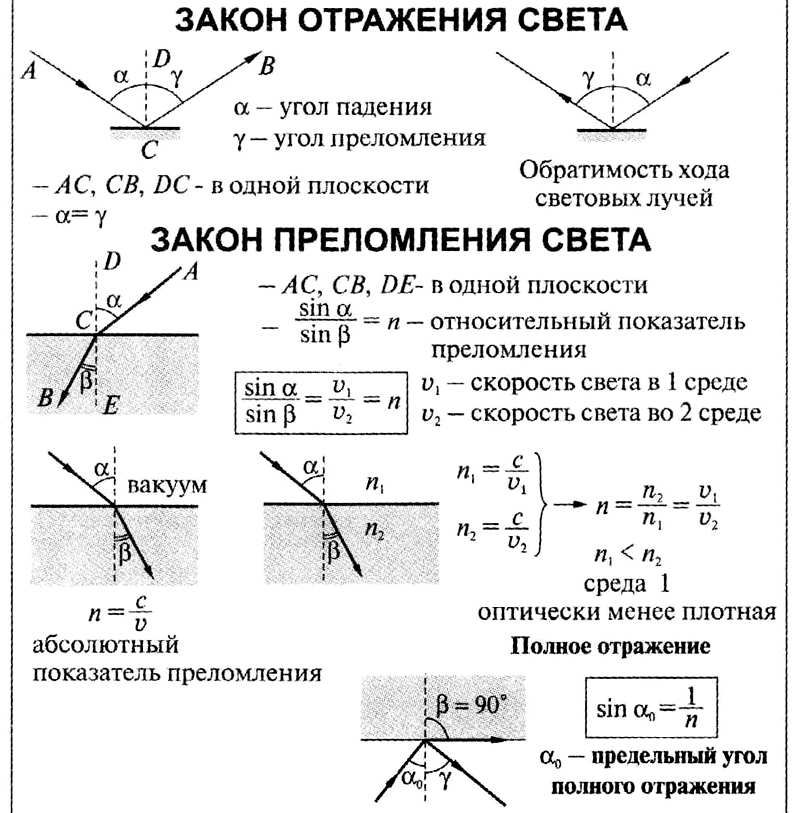
Закон отражения света, основывается на том, что падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, находятся в одной плоскости (плоскость падения). При этом углы отражения и падения, γ и α – соответственно, являются равными величинами.

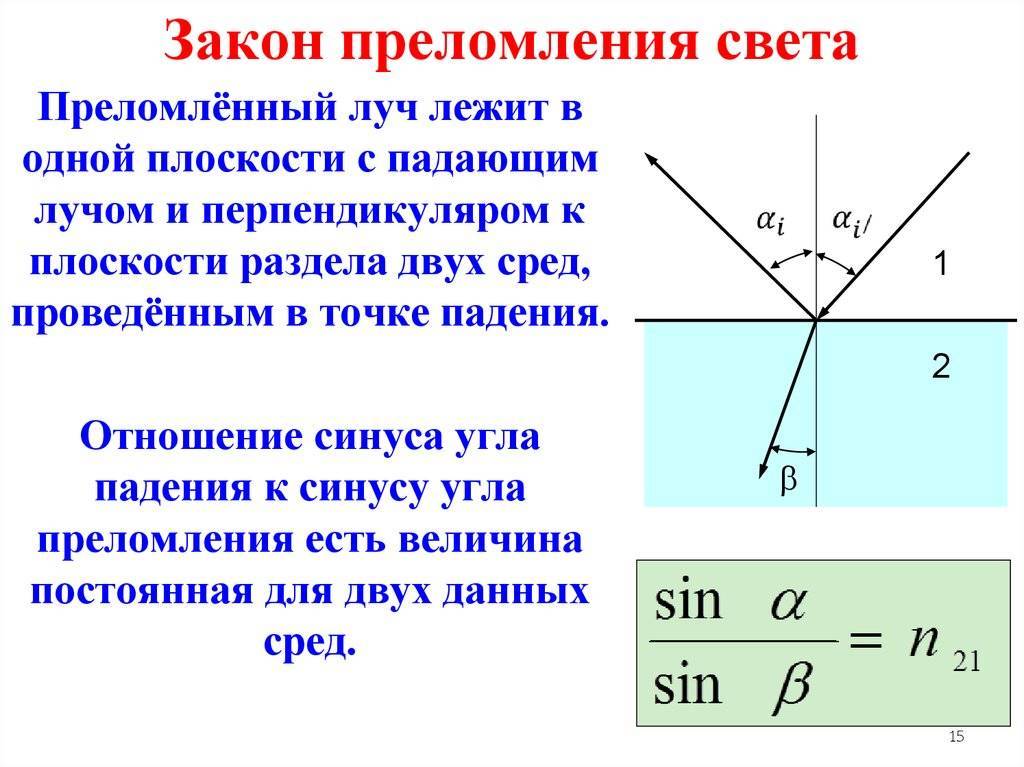
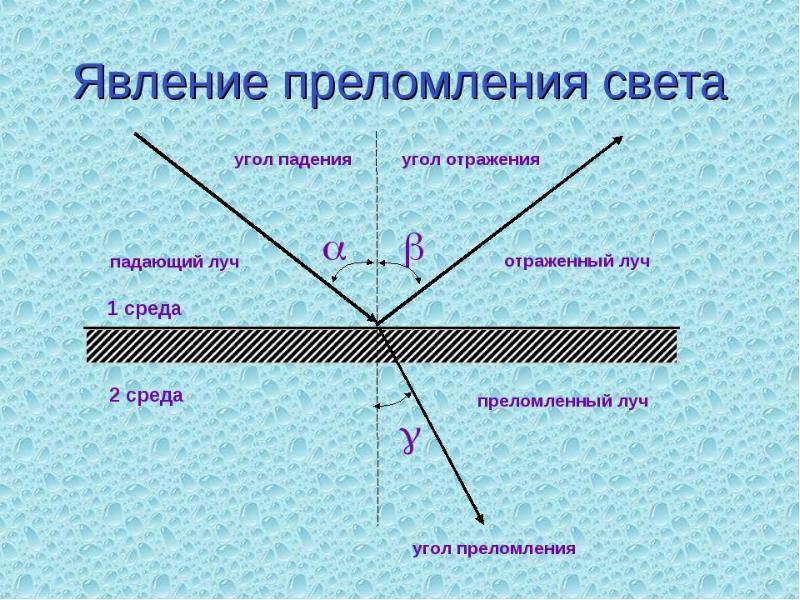
Закон преломления света

Определение 4

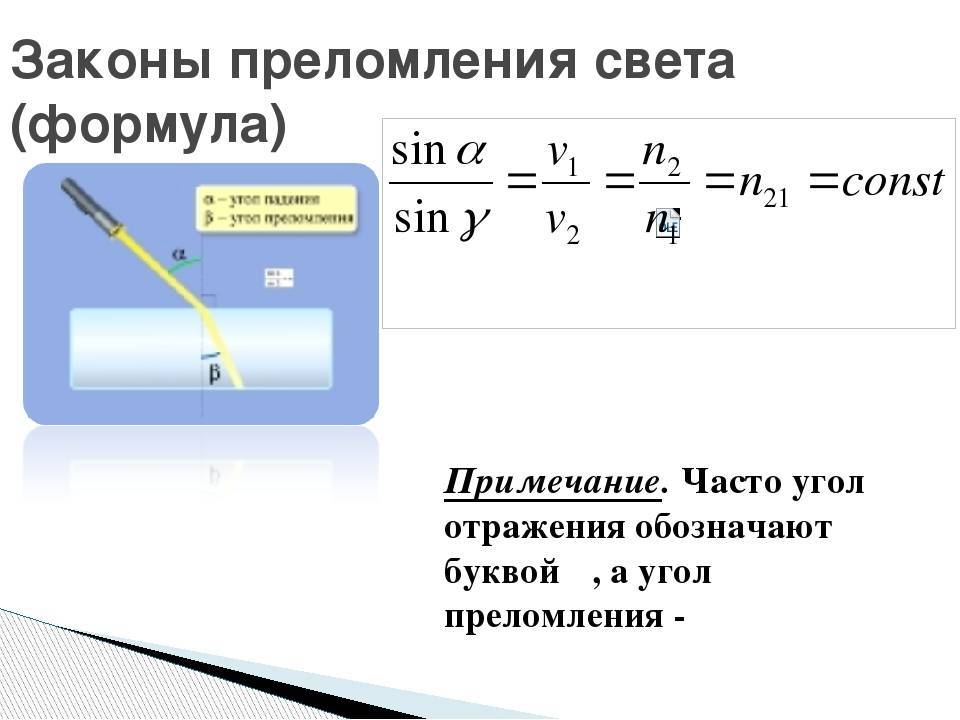
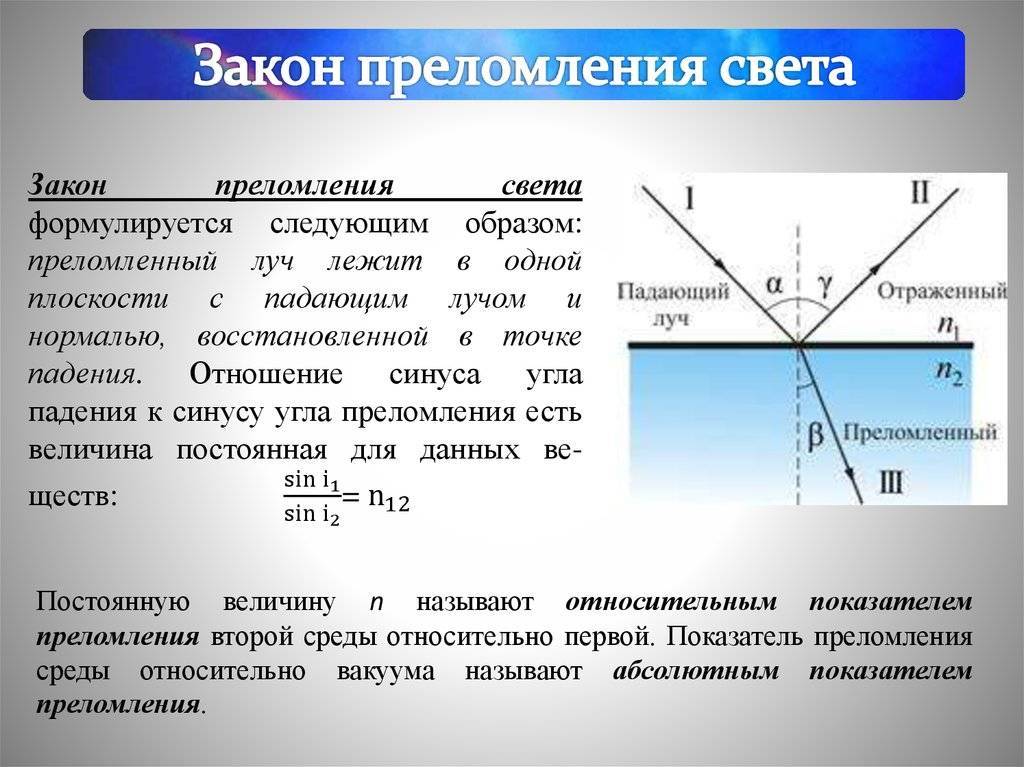
Закон преломления света, базируется на том, что падающий и преломленный лучи, также как перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение sin угла падения α к sin угла преломления β является величиной, неизменной для двух приведенных сред:

sin αsin β=n.

Ученый В. Снеллиус экспериментально установил закон преломления в 1621 году.

Определение 5

Постоянная величина n – является относительным показателем преломления второй среды относительно первой.

Определение 6

Показатель преломления среды относительно вакуума имеет название – абсолютный показатель преломления.

Определение 7

Относительный показатель преломления двух сред – это отношение абсолютных показателей преломления данных сред, т.е.: 

n = n2n1.

Свое значение законы преломления и отражения находят в волновой физике. Исходя из ее определений, преломление является результатом преобразования скорости распространения волн в процессе перехода между двумя средами.

Определение 8

Физический смысл показателя преломления – это отношение скорости распространения волн в первой среде υ1 к скорости во второй υ2:

n=υ1υ2.

Определение 9

Абсолютный показатель преломления эквивалентен отношению скорости света в вакууме c к скорости света υ в среде: 

n=cυ.

На рисунке 3.1.1 проиллюстрированы законы отражения и преломления света.

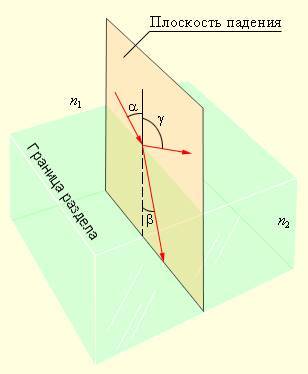
Рисунок 3.1.1. Законы отражения υ преломления: γ = α; n1 sin α=n2 sin β.

Определение 10

Среда, абсолютный показатель преломления которой является меньшим, является оптически менее плотной.

Определение 11

В условиях перехода света из одной среды, уступающей в оптической плотности другой (n2<n1) мы получаем возможность наблюдать явление исчезновения преломленного луча.

Данное явление можно наблюдать при углах падения, которые превышают некий критический угол αпр. Этот угол носит название предельного угла полного внутреннего отражения (см. рис. 3.1.2).

Для угла падения α=αпр  sin β=1; значение sin αпр=n2n1< 1.

При условии, что второй средой будет воздух (n2≈1), то равенство будет допустимо переписать в вид: sin αпр=1n, где n=n1>1 – абсолютный показатель преломления первой среды.

В условиях границы раздела «стекло–воздух», где n=1,5, критический угол равен αпр=42°, в то время как для границы «вода–воздух» n=1,33, а αпр=48,7°.

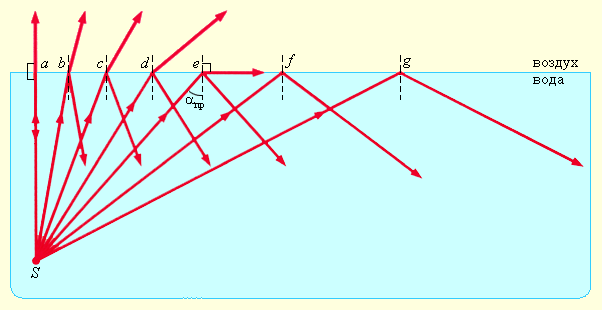
Рисунок 3.1.2. Полное внутреннее отражение света на границе вода–воздух; S – точечный источник света.

Закон преломления света

Из принципа Ферма можно получить и закон преломления света (точнее — световых лучей). Здесь речь идет о переходе света из одной среды (среда I на рисунке 4) в другую (среда II) через границу раздела между ними. Различие сред состоит в том, что в них различны скорости распространения света.

Рис. 4

Мы рассмотрим случай, когда среда I — это вакуум, в котором скорость света равна с, а вторая среда — какое-то прозрачное вещество (например, стекло, вода и т. д.), в котором скорость света υ меньше, чем с : с > υ.

Между точками А в среде I и В в среде II также мыслимы бесчисленное множество путей, но, согласно принципу Ферма, свет «выбирает» тот из них, для прохождения которого нужно наименьшее время. Ясно, например, что путь АА’В не есть такой путь, потому что здесь свет проходит короткое (кратчайшее) расстояние в среде с большой скоростью и большое расстояние в среде с малой скоростью. Быть может, выгоднее путь АВ’В? Здесь свет в среде с малой скоростью проходит минимальную часть пути, а наибольшая часть приходится на среду с большой скоростью. Но есть ли именно этот путь самый выгодный в смысле экономии времени? Может быть, выгоднее несколько удлинить путь в среде II с тем, чтобы сократить путь в среде I? Словом, нужно найти, в какой точке свету (лучу) нужно пересечь границу раздела двух сред, чтобы время прохождения от А к В было наименьшим. Ясно, что эта точка лежит где-то между А’ и В’ (включая, возможно, и самую точку В’).

Обозначим расстояние между А’ и В’ через d. Если нужная нам точка С пересечения границы раздела находится на расстоянии х от А’, то от В’ она отстоит на расстоянии d — х (см. рис. 4). Путь АС, проходимый светом в среде I, равен \(~\sqrt{y^2_1 + x^2}\), а время прохождения этого пути

\(~t_1 = \frac{\sqrt{y^2_1 + x^2}}{c}\) .

Путь СВ, проходимый светом в среде II, равен \(~\sqrt{y^2_2 + (x – d)^2}\), а время, нужное для прохождения этого пути,

\(~t_2 = \frac{\sqrt{y^2_2 + (x – d)^2}}{\upsilon}\) .

Общее время t определяется равенством

\(~t = t_1 + t_2 = \frac{\sqrt{y^2_1 + x^2}}{c} + \frac{\sqrt{y^2_2 + (x – d)^2}}{\upsilon}\) . (1)

Время t зависит только от х — координаты точки падения луча, так как величины y₁, y₂, с, υ и d — постоянные, то есть одинаковые при всех значениях х. Вот нам и нужно найти, при каком значении х время t будет наименьшим. Средствами обычной алгебры эту задачу решить нельзя. Чтобы ее решить, нужно воспользоваться тем, что при том значении х, при котором t минимально, производная функции, стоящей в правой части уравнения (1), равна нулю.

Это приводит нас к такому условию для х:

\(~\frac{x}{c\sqrt{y^2_1 + x^2}} = \frac{d – x}{\upsilon \sqrt{y^2_2 + (x – d)^2}}\) . (2)

Из рисунка 4 видно, что

\(~\frac{x}{\sqrt{y^2_1 + x^2}} = \sin \angle A’AC = \sin \alpha ; \frac{d – x}{\sqrt{y^2_2 + (x – d)^2}} = \sin \angle CBB’ = \sin \beta\) .

где α — угол между падающим лучом и нормалью к границе раздела в точке падения (угол падения) и β — угол между этой нормалью и преломленным лучом (угол преломления). Условие (2) принимает поэтому вид:

\(~\frac{\sin \alpha}{c} = \frac{\sin \beta}{\upsilon}\) или \(~\frac{\sin \alpha}{\sin \beta} = \frac{c}{\upsilon}\) .

В этом и заключается закон преломления для нашего случая: отношение синуса угла падения к синусу угла преломления равно отношению скоростей распространения света в вакууме и в среде, которая с ним граничит. Отношение \(~\frac{c}{\upsilon}\) — величина постоянная, характерная для данной среды. Она называется показателем преломления вещества и обозначается буквой n, так что

\(~\frac{\sin \alpha}{\sin \beta} = n\) .

В общем случае, когда свет переходит из произвольной среды, в которой скорость света равна υ₁, в среду со скоростью света в ней υ₂, закон преломления имеет вид

\(~\frac{\sin \alpha}{\sin \beta} = \frac{\upsilon_1}{\upsilon_2} = n_{21}\) ,

где n₂₁ — относительный показатель преломления сред 2 и 1.

Принцип Ферма справедлив, конечно, не только для тех простейших примеров отражения и преломления света, которые мы здесь рассмотрели. С помощью этого принципа можно понять и точно рассчитать ход лучей и в призме, и в линзе и в любой самой сложной системе призм, линз, зеркал.

Зеркальное и диффузионное отражение

Отражающая поверхность может быть гладкой, но также может иметь и неровности. В связи с этим различают два типа отражения света:

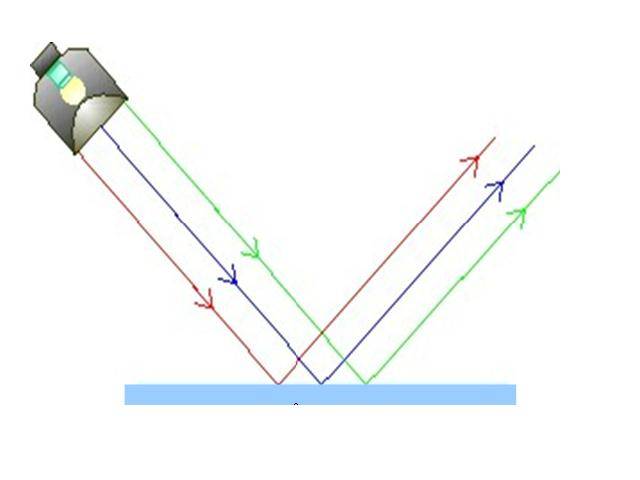
1. Зеркальное. Если неровности на отражающей поверхности малы по сравнению с длиной падающей волны, тогда пучок света отражается в определенном направлении. Здесь можно привести пример поверхности плоского зеркала, закона отражения света для которой можно применять.
2. Диффузионное. Если неровности поверхности сравнимы с длиной световой волны, тогда каждая часть падающего пучка отражается от различных неровностей, при этом закон отражения света остается справедливым для каждого факта отражения, но поскольку отраженные пучки света начинают распространяться в различных направлениях, получается, что начальный пучок распадается на множество мелких пучков. В таких случаях говорят, что свет рассеивается. Примером диффузионного отражения является отражение света от деревянной поверхности.

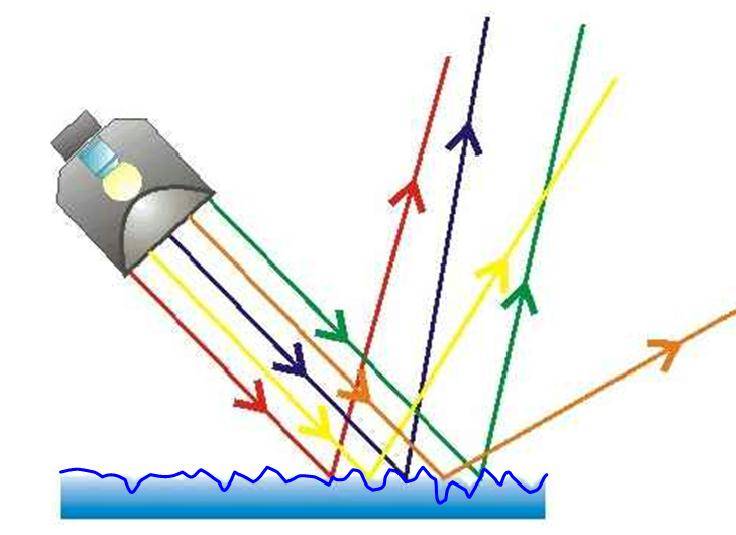
Таким образом, если после зеркального отражения свет распространяется в конкретном направлении, то после диффузионного отражения свет “распыляется”.

Механизм отражения

В классической электродинамике, свет рассматривается как электромагнитная волна, которая описывается уравнениями Максвелла. Световые волны, падающие на диэлектрик вызывают малые колебания диэлектрической поляризации в отдельных атомах, в результате чего каждая частица излучает вторичные волны во всех направлениях (как антенна-диполь). Все эти волны складываются и в соответствии с принципом Гюйгенса — Френеля дают зеркальное отражение и преломление. При попадании электромагнитной волны на проводящую поверхность возникают колебания электронов (электрический ток), электромагнитное поле которого стремится компенсировать это воздействие, что приводит к практически полному отражению света.

В зависимости от резонансной частоты колебательных контуров в молекулярной структуре вещества при отражении излучается волна определённой частоты (определённого цвета). Так предметы приобретают цвет. Хотя цвет объекта определяется не только свойствами отражённого света (см. Цветовое зрение и Физиология восприятия цвета).

Ретроотражение и оптические аберрации

Под оптической аберрацией понимают явление в физике, при котором полученное в какой-либо оптической системе изображение оказывается нечетким. Происходит это потому, что выходящий из определенной точки объекта луч света не возвращается точно в одну точку. Причинами аберрации могут быть геометрические несовершенства оптических систем, а также различная отражающая способность для разных длин волн видимого света.

Ретроотражение используется для нивелирования оптических аберраций. Делается это простым образом, полученное в оптической системе изображение объекта через ретроотражатель заново направляется в эту систему. Функция ретроотражателя заключается не только в том, что он обратно возвращает все падающие на него лучи, но и меняет волновой фронт электромагнитной волны на противоположный.

Законы отражения света

Под отражением света в физике понимают такое изменение направления распространения волны, после того как она падает на границу между двумя средами, при котором волна снова возвращается в среду, откуда она пришла.

После того как сформулирован закон отражения света, отметим, что благодаря существованию этого явления можно видеть изображения разных предметов в зеркале, на поверхности воды или на какой-либо другой блестящей поверхности. Физически отражение света происходит, когда свет падает на какую-либо поверхность, сталкивается с ней и снова возвращается в первоначальную среду своего распространения, образуя угол, в точности равный углу падающего на эту поверхность луча. Эта поверхность называется отражающей. В отличие от явления преломления, феномен отражения – это изменение направления распространения волны в той же самой среде.

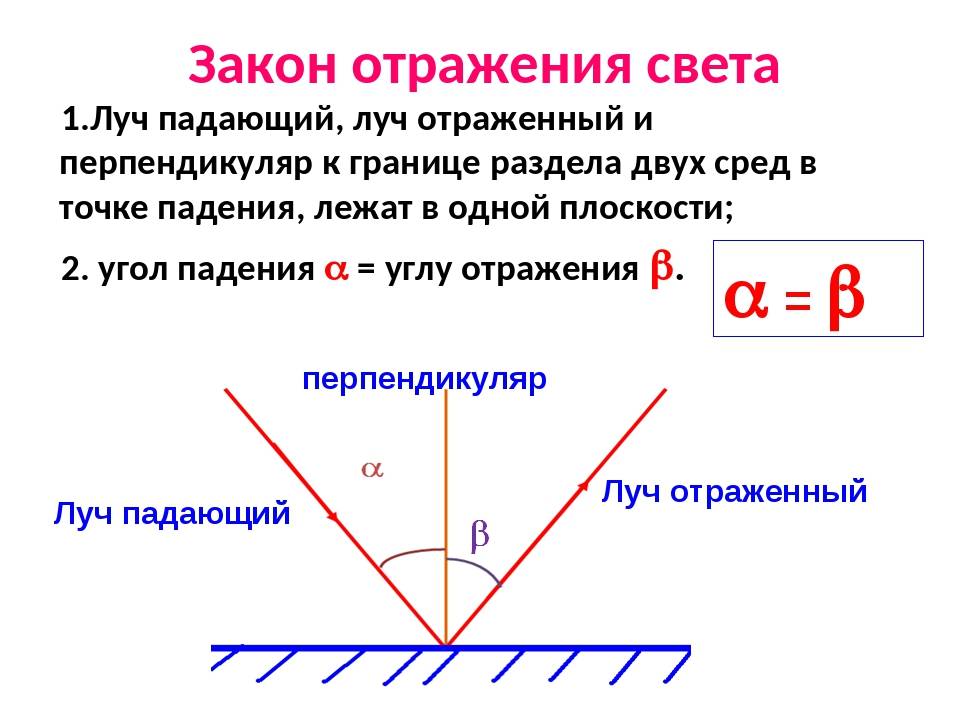
В физике законы отражения света формулируются следующим образом:

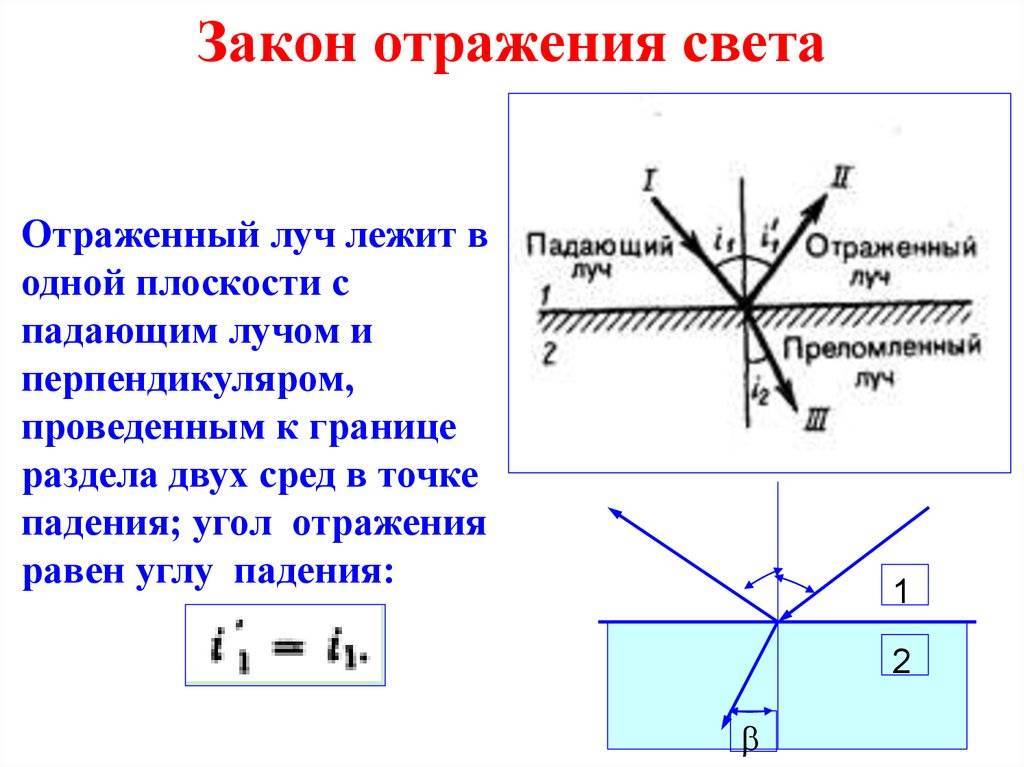
1. Падающий на поверхность раздела сред луч, отраженный луч и нормаль к этой поверхности лежат в одной плоскости.
2. Угол падения равен углу отражения. Формула закона отражения света имеет вид: θ_пад. = θ_отр..

Вывод Закона Отражения Света из Принципа Ферма

Принцип Ферма Геометрическая оптика может быть построена, исходя из разных принципов. С одной стороны мы можем воспользоваться законами отражения и преломления, с другой – можно использовать принцип Ферма или принцип Гюйгенса. С законами отражения и преломления мы работали уже достаточно долго, а сейчас обсудим принцип Ферма.

Рассмотрим оптическую среду, в которой скорость света меняется от точки к точке , такая среда называется неоднородной.

Можно сказать, что скорость света зависит от точки, а можно сказать, что показатель преломления зависит от точки . Это одно и то же, т.к. они связаны соотношением , где постоянная – скорость света в вакууме.

В неоднородной среде световые лучи не движутся по прямым, они искривляются.

Рис. 2. Один из лучей, выходящих ииз точки , попадает в точку

Проведем все возможные пути из точки в точку , в том числе и сам световой луч.

Рис. 3. Все пути из в , среди них красным отмечен световой луч

Часто вместо времени прохождения оперируют с оптической длиной пути

. Т.к. оптическая длина и время прохождения пропорциональны между собой

(коэффициентом пропорциональности служит скорость света в вакууме ), принцип Ферма может быть сформулирован и следующим образом

оптическая длина светового луча, идущего из одной точки в другую, наименьшая по сравнению со всеми другими путями, соединяющими эти точки. На самом деле обе данные нами формулировки принципа Ферма требуют некоторого уточнения – вместо слова наименьшее в них должно стоять слово стационарное, но сейчас мы не будем на этом останавливаться.

А теперь покажем, что из принципа Ферма следуют все основные законы геометрической оптики.

Этот выбор осуществляют с помощью следующего геометрического приема. Отразим точку в зеркале . Основное геометрическое утверждение состоит в следующем: для любой точки на зеркале длины ломаных и равны.

Введем систему координат, в которой ось идет вдоль границы раздела сред, а ось проходит через точку . Будем считать, что , и .

На самом деле имеется единственная возможность устранить это противоречие – предположить, что время прохождения всех этих лучей одно и то же и, кроме того, оно минимально по отношению к времени прохождения всех других путей, соединяющих эти две точки.

Этот принцип, являющийся следствием принципа Ферма, называется принципом таутохронности или принципом равновремённости. Приступим к конструированию нашего устройства. Самый примитивный эскиз может выглядеть следующим образом

Рис. 7. Первый набросок устройства, собирающего все лучи в одну точку

Ясно, что эта неверна, т.к. средний луч проходится за наименьшее время и свет пойдет только по нему. В силу принципа таутохронности мы должны уравнять время прохождения всех лучей. Для этого поставим на пути каждого луча замедлитель – кусок стекла, там скорость в полтора раза меньше, чем в воздухе. Для коротких лучей замедлитель (кусок стекла) должен быть потолще, для длинных – потоньше.

Принцип Ферма. Законы отражения и преломления Понятно, что полученное устройство – это примитивный прообраз линзы. На самом деле тут не так уж далеко до точного расчета формы идеальной линзы.

Мнение эксперта It-Technology, Cпециалист по электроэнергетике и электронике Задавайте вопросы “Специалисту по модернизации систем энергогенерации”

Принцип Гюйгенса. Принцип Ферма. Законы отражения света — презентация, доклад, проект Мы должны потребовать, чтобы длины всех этих лучей были одинаковы и минимальны по отношению к длинам всех других путей, соприкасающихся с отражающей кривой и соединяющих эти две точки. Спрашивайте, я на связи!