Сила Лоренца и правило левой руки. Движение заряженных частиц в магнитном поле

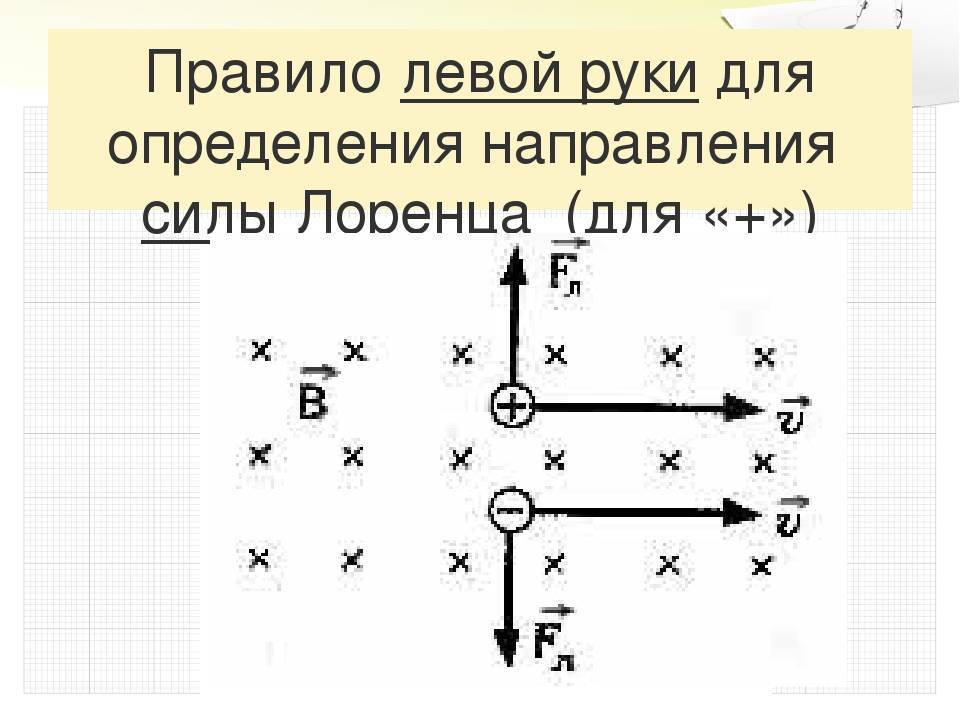
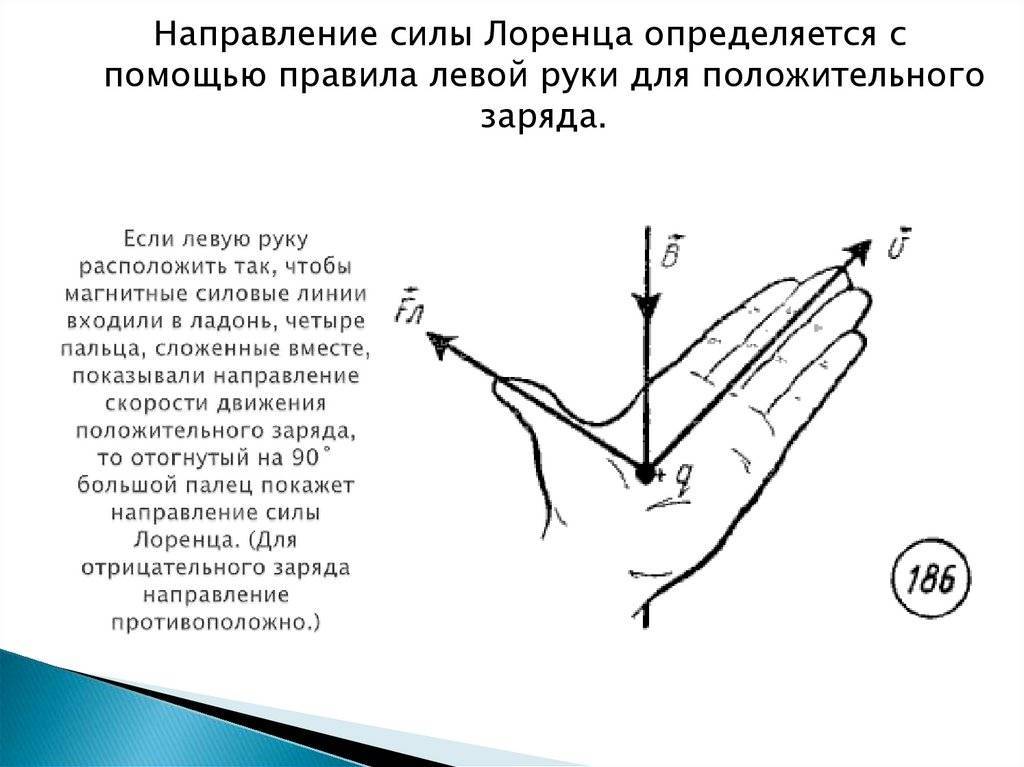
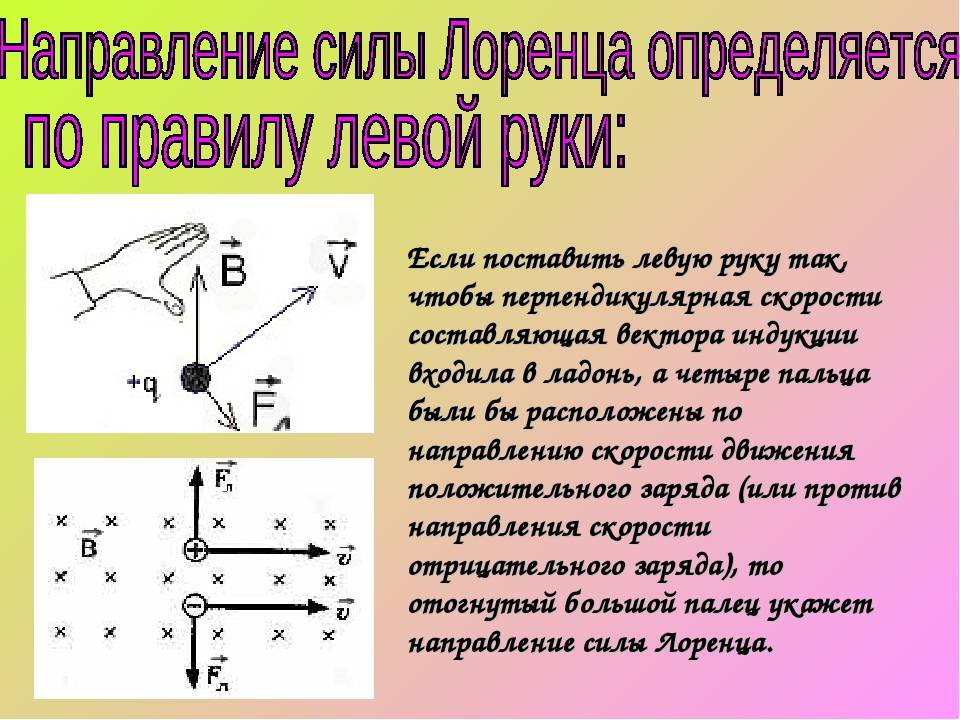
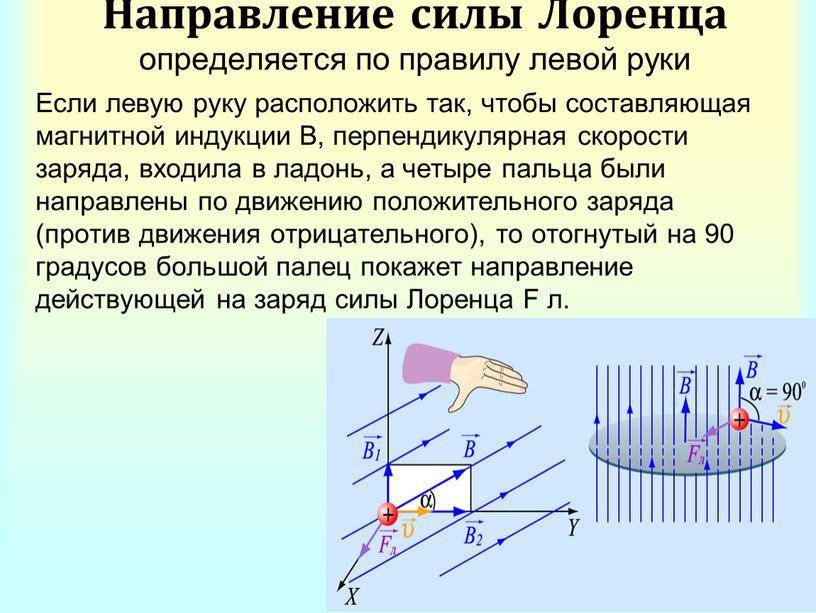
Широкое применение

Первыми приборами для предполагаемых открытий стали циклотроны. Смысл их работы довольно прост: частицы двигаются полукругом. Каждый раз, когда они проходят определённую область, специальный модуль включает электрическое поле, чтобы ускорить их.

Масс-спектрометры применяются для идентификации атомов и молекул. Они используются в следующих устройствах:

• электродвигатели;
• громкоговорители;
• рельсовые пистолеты.

Способность силы Лоренца связывать механическое смещение с электрическим током представляет большой интерес для медицинской акустики. Например, разрабатывался гидрофон для картирования скорости частиц акустического поля. Предполагалось, что он будет построен с использованием тонкого медного провода и внешнего магнитного поля.

Созданный прототип был охарактеризован. Было исследовано его пространственное разрешение, частотная характеристика, чувствительность, надёжность и характеристика направленности. Был также изучен метод визуализации, называемый электрической импедансной томографией. В этом методе биологическая ткань вибрирует ультразвуком в магнитном поле, которое индуцирует электрический ток. Этот метод был применён для визуализации желатинового фантома, образца мышц говядины и термического поражения в образце куриной грудки. Это показало, что метод может быть полезен для обеспечения дополнительного контраста по сравнению с обычной ультразвуковой визуализацией.

Применение силы Лоренца

Определение 3

Приведенное снизу соотношение представляет собой формулу угловой скорости движения заряженной частицы, происходящего по круговой траектории:

ω=υR=υqBmυ=qBm.

Оно носит название циклотронной частоты. Данная физическая величина не имеет зависимости от скорости частицы, из чего можно сделать вывод, что и от ее кинетической энергии она не зависит.

Определение 4

Данное обстоятельство находит свое применение в циклотронах, а именно в ускорителях тяжелых частиц (протонов, ионов).

На рисунке 1.18.3 приводится принципиальная схема циклотрона.

Рисунок 1.18.3. Движение заряженных частиц в вакуумной камере циклотрона.

Определение 5

Дуант – это полый металлический полуцилиндр, помещенный в вакуумную камеру между полюсами электромагнита в качестве одного из двух ускоряющих D-образного электрода в циклотроне.

К дуантам приложено переменное электрическое напряжение, чья частота эквивалентна циклотронной частоте. Частицы, несущие некоторый заряд, инжектируются в центре вакуумной камеры. В промежутке между дуантами они испытывают ускорение, вызываемое электрическим полем. Частицы, находящиеся внутри дуантов, в процессе движения по полуокружностям испытывают на себе действие силы Лоренца. Радиус полуокружностей возрастает с увеличением энергии частиц. Как и во всех других ускорителях, в циклотронах ускорение заряженной частицы достигается путем применения электрического поля, а ее удержание на траектории с помощью магнитного поля. Циклотроны дают возможность ускорять протоны до энергии, приближенной к 20 МэВ.

Однородные магнитные поля используются во многих устройствах самых разных типов назначений. В частности, они нашли свое применение так называемых масс-спектрометрах.

Определение 6

Масс-спектрометры – это такие устройства, использование которых позволяет нам измерять массы заряженных частиц, то есть ионов или ядер различных атомов.

Данные приборы используются для разделения изотопов (ядер атомов с одинаковым зарядом, но разными массами, к примеру, Ne20 и Ne22). На рис. 1.18.4 изображен простейшая версия масс-спектрометра. Вылетающие из источника S ионы проходят через несколько малых отверстий, которые в совокупности формируют узкий пучок. После этого они попадают в селектор скоростей, где частицы движутся в скрещенных однородных электрическом, создающимся между пластинами плоского конденсатора, и магнитном, возникающим в зазоре между полюсами электромагнита, полях. Начальная скорость υ→ заряженных частиц направлена перпендикулярно векторам E→ и B→.

Частица, которая движется в скрещенных магнитном и электрическом полях, испытывает на себе воздействия электрической силы qE→ и магнитной силы Лоренца. В условиях, когда выполняется E=υB, данные силы полностью компенсируют воздействие друг друга. В таком случае частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, которые движутся со скоростью υ=EB.

После данных процессов частицы с одинаковыми значениями скорости попадают в однородное магнитное поле B→ камеры масс-спектрометра. Частицы под действием силы Лоренца движутся в камере перпендикулярной магнитному полю плоскости. Их траектории представляют собой окружности с радиусами R=mυqB’. В процессе измерения радиусов траекторий при известных значениях υ и B’, мы имеем возможность определить отношение qm. В случае изотопов, то есть при условии q1=q2, масс-спектрометр может разделить частицы с разными массами.

С помощью современных масс-спектрометров мы имеем возможность измерять массы заряженных частиц с точностью, превышающей 10–4.

Рисунок 1.18.4. Селектор скоростей и масс-спектрометр.

Взаимодействие токов

Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.

В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:

Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.

Во втором случае магнитная индукция в центре кругового витка с током равна:

Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.

Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Что означает сила и ее формула

Силой Лоренца принято называть силу, влияющую на электрон, который движется и находится в магнитном поле. Речь идет о комбинации двух сил – магнитной, электрической, сконцентрированных на заряде. Сила Лоренца определяется следующими значениями:

• индукцией;
• величиной заряда;
• скоростью передвижения частицы.

Направление заряженной частицы ортогонально плоскости, где находятся векторы скорости перемещения. Для силы Лоренца в физике существует равнодействующая сила – это сила Ампера.

Для наглядной демонстрации искомой силы давайте вспомним опыт, который вам наверняка показывали на уроке физики — с магнитом, опилками металла, листом бумаги. Преподаватель подносил магнит к опилкам снизу, через бумагу и они выстраивались по четким линиям. Именно они образуют силовое поле магнита. Примечательно, что это замкнутое пространство без начала и конца. Речь идет о векторной величине, которая при любых обстоятельствах устремляется в сторону северного полюса магнита. Если в поле попадает заряженная частица, происходит смена траектории. Угол отклонения определяется скоростью движения частицы, а также силой, которая влияет на электрон. Это и есть искомая сила Лоренца, для ее вычисления применяют формулу: FЛ=qVB, здесь:

• q – сила заряда (обозначается в Кулонах);
• V – скорость передвижения заряда (обозначается в м/с);
• В — индукция поля (обозначается в Тесла).

Определение силы, а также формула, предложенные в конце 19 столетия, актуальны и сегодня.

Направление силы

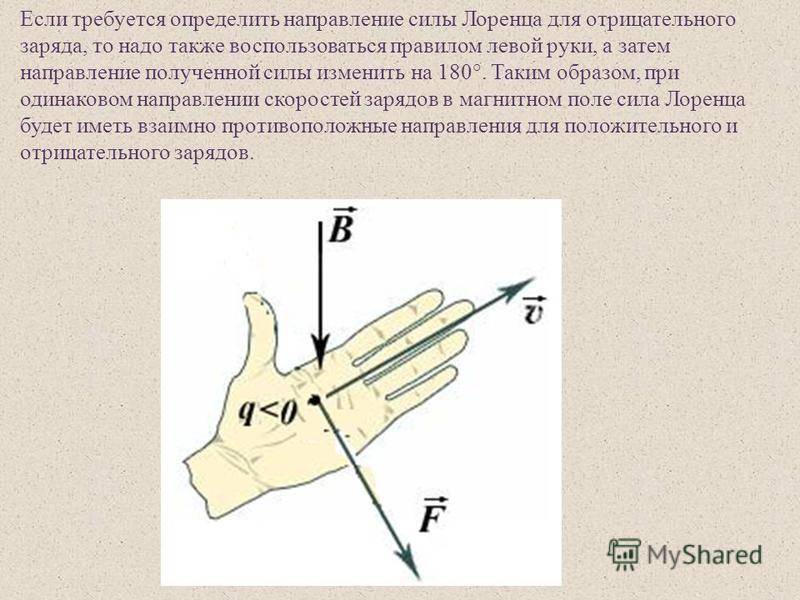
Указание силы Лоренца становится противоположным при соблюдении двух условий:

• когда знак заряда также становится противоположным;
• направления других векторов остаются неизменными.

Траекторию электрона принято называть винтовой линией.

Когда возникает

Параметры магнитного поля остаются неизменными, если заряженная частица неподвижна. Аналогично на проводник не действует сила Ампера, когда нет тока.

Чтобы определить модуль силы Лоренца потребуется соблюдение таких условий:

1. наличие заряда у частицы;

2. наличие магнитного поля;

3. частица должна двигаться.

Если не выполняется одно из трех условий, сила отсутствует.

Закон силы тяжести

Замечание 1 Сила тяжести является одним из случаев проявления действия гравитационных сил.

Силу тяжести представляют в виде такой силы, которая действует на тело со стороны планеты и придает ему ускорение свободного падения.

Свободное падение можно рассмотреть в виде $mg = G\frac{mM}{r^2}$, откуда получаем формулу ускорения свободного падения:

$g = G\frac{M}{r^2}$.

Формула определения силы тяжести будет выглядеть следующим образом:

${\overline{F}}_g = m\overline{g}$

Сила тяжести имеет определенный вектор распространения. Он всегда направлен вертикально вниз, то есть по направлению к центру планеты. На тело действует силы тяжести постоянно и это означает, что оно совершает свободное падение.

Траектория движения при действии силы тяжести зависит от:

Готовые работы на аналогичную тему

• Курсовая работа Законы силы, формулы 490 руб.
• Реферат Законы силы, формулы 250 руб.
• Контрольная работа Законы силы, формулы 210 руб.

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

• модуля начальной скорости объекта;
• направления скорости движения тела.

С этим физическим явлением человек сталкивается ежедневно.

Силу тяжести можно также представить в виде формулы $P = mg$. При ускорении свободного падения учитываются также дополнительные величины.

Если рассматривать закон всемирного тяготения, который сформулировал Исаак Ньютон, все тела обладают определенной массой. Они притягиваются друг к другу с силой. Ее назовут гравитационной силой.

$F = G\frac{m_1m_2}{r^2}$

Эта сила прямо пропорциональна произведению масс двух тел и обратно пропорциональна квадрату расстояния между ними.

$G = 6,7\cdot {10}^{-11}\ {H\cdot m^2}/{{kg}^2\ }$, где $G$ — это гравитационная постоянная и она имеет по международной системе измерений СИ постоянное значение.

Определение 1

Весом называют силу, с которой тело действует на поверхность планеты после возникновения силы тяжести.

В случаях, когда тело находится в состоянии покоя или равномерно движется по горизонтальной поверхности, тогда вес будет равен силе реакции опоры и совпадать по значению с величиной силы тяжести:

Лень читать?

Задай вопрос специалистам и получи ответ уже через 15 минут!

Задать вопрос

$Р = тg$

При равноускоренном движении вертикально вес будет отличаться от силы тяжести, исходя из вектора ускорения. При направлении вектора ускорения в противоположную сторону возникает состояние перегрузки. В случаях, когда тело вместе с опорой двигаются с ускорением $а = g$, тогда вес будет равен нулю. Состояние с нулевым весом называют невесомостью.

Напряженность поля тяготения высчитывается следующим образом:

$g = \frac{F}{m}$

Величина $F$ — сила тяготения, которая действует на материальную точку массой $m$.

Тело помещается в определенную точку поля.

Потенциальная энергия гравитационного взаимодействия двух материальных точек, имеющих массы $m_1$ и $m_2$, должны находиться на расстоянии $r$ друг от друга.

Потенциал поля тяготения можно найти по формуле:

$\varphi = \Pi / m$

Здесь $П$ — потенциальная энергия материальной точки с массой $m$. Она помещена в определенную точку поля.

Обнаружение МП по его действию на эл. ток. Правило левой руки

Поскольку магнитное поле проводника с током действует с определённой силой на магнит, то естественно предположить, что со стороны магнитного поля магнита на проводник с током также должна действовать какая-то сила. Рассмотрим более подробно действие магнитного поля на проводник с током и попытаемся подтвердить или опровергнуть высказанное предположение.

Для этого соберём цепь, состоящую из источника тока, ключа, трёхсторонней рамки, реостата и подковообразного магнита, закреплённого в штативе. Рамку подвесим на крючках так, чтобы она могла свободно вращаться, и поместим в магнитное поле, созданное подковообразным магнитом. Присоединим рамку к источнику тока, последовательно с реостатом и ключом. При разомкнутой цепи действия со стороны магнитного поля магнита на рамку не наблюдается. Если же цепь замкнуть, то проводник приходит в движение — он втягивается в пространство между полюсами дугообразного магнита.

Следовательно, магнитное поле действует на рамку с током с некоторой силой

, отклоняющей её от первоначального положения.

Раз магнитное поле способно оказывать действие на проводник с током, то это действие может быть использовано для обнаружения магнитного поля в данной области пространства.

Кто-то из вас скажет, что зачем столько сложностей, если магнитное поле можно обнаружить с помощью простого компаса.

Да, с помощью компаса проще, но вспомните гипотезу Ампера: внутри каждой молекулы вещества циркулируют кольцевые электрические токи.

Поэтому действие магнитного поля на стрелку компаса сводится к действию поля на элементарные электрические токи, которые циркулируют в атомах и молекулах вещества, из которого изготовлена магнитная стрелка.

Таким образом, магнитное поле создаётся электрическим током и обнаруживается по его действию на электрический ток.

Но вернёмся к нашему опыту. Давайте поменяем направление тока в цепи. Замкнув её увидим, что проводник отклонился в противоположную сторону.

Значит, вместе с током изменилось и направление действующей на рамку силы.

Если теперь поменять местами полюсы магнита (то есть изменить направление магнитных линий), то мы увидим, как рамка с током вновь втягивается в пространство между полюсами магнита.

Значит, направление тока в проводнике, направление линий магнитного поля и направление силы, действующей на проводник с током, связаны между собой.

Из курса физики восьмого класса вы знаете, что сила, с которой магнитное поле действует на помещённый в него проводник с током, называется силой Ампера,

в честь французского учёного Андре-Мари Ампера.

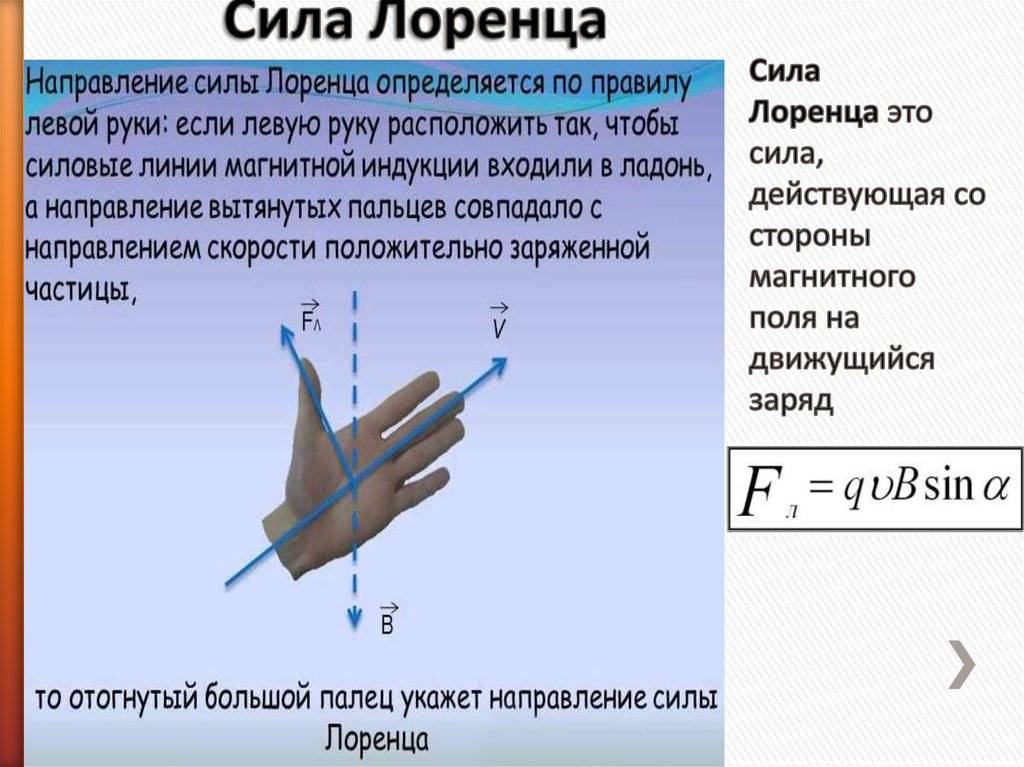
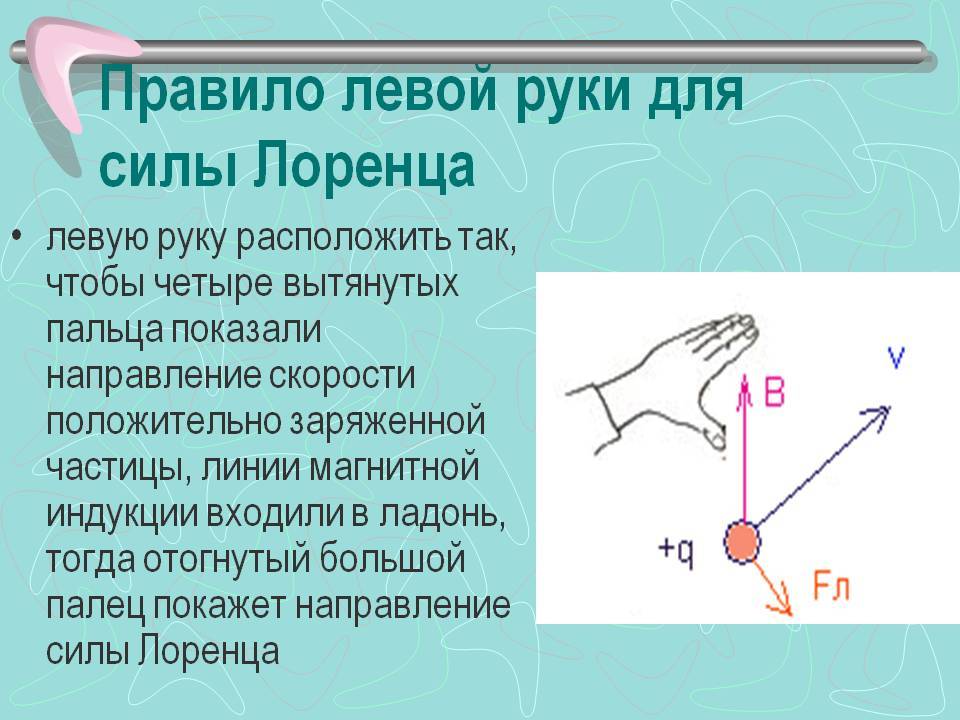
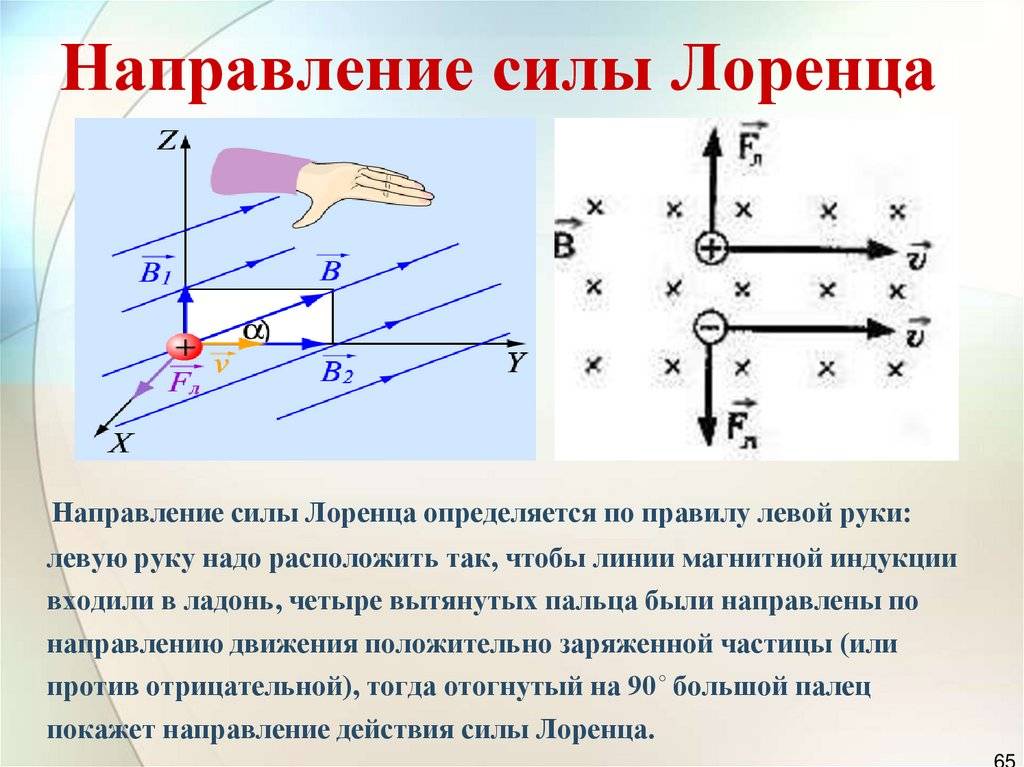
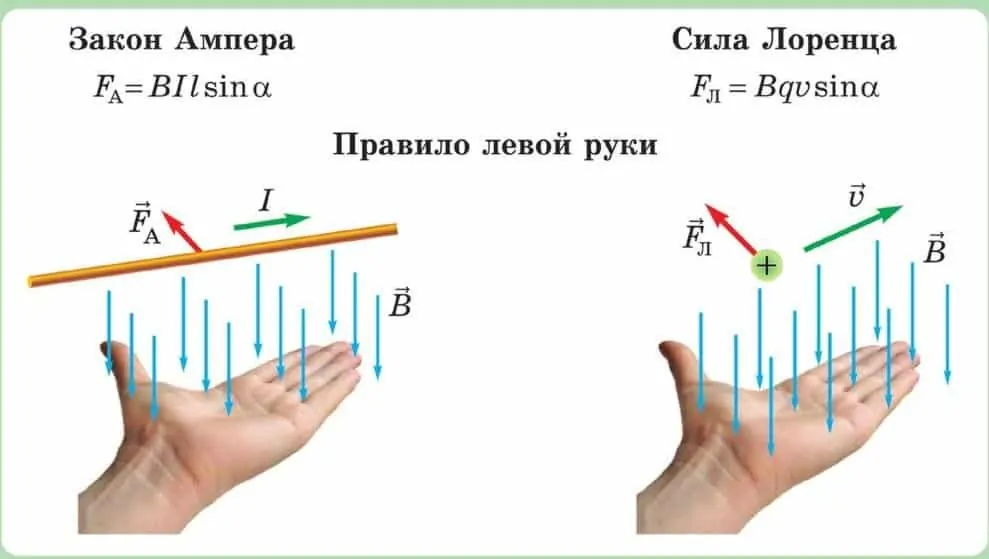
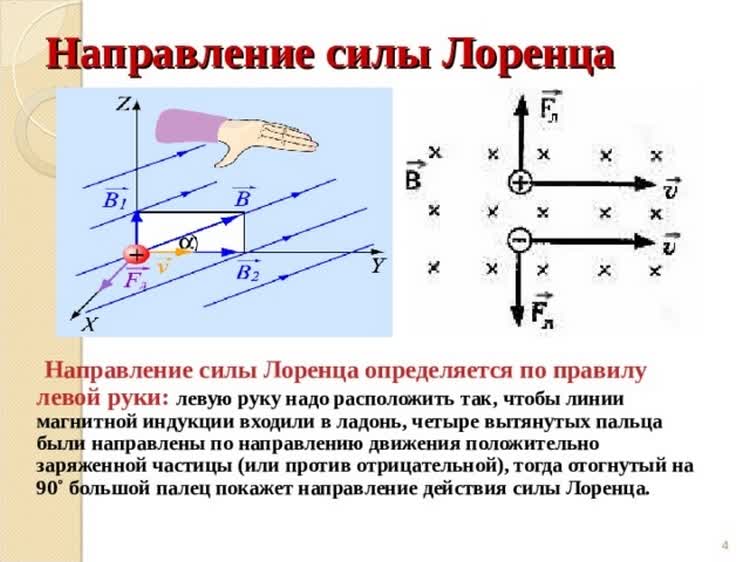
Направление силы Ампера можно определить с помощью правила левой руки: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь, а четыре пальца были направлены по направлению тока в проводнике, то отогнутый на девяносто градусов большой палец покажет направление действующей на проводник силы.

При использовании данного правила не забывайте о том, что за направление тока в цепи принято направление в котором движутся или могли бы двигаться положительно заряженные частицы.

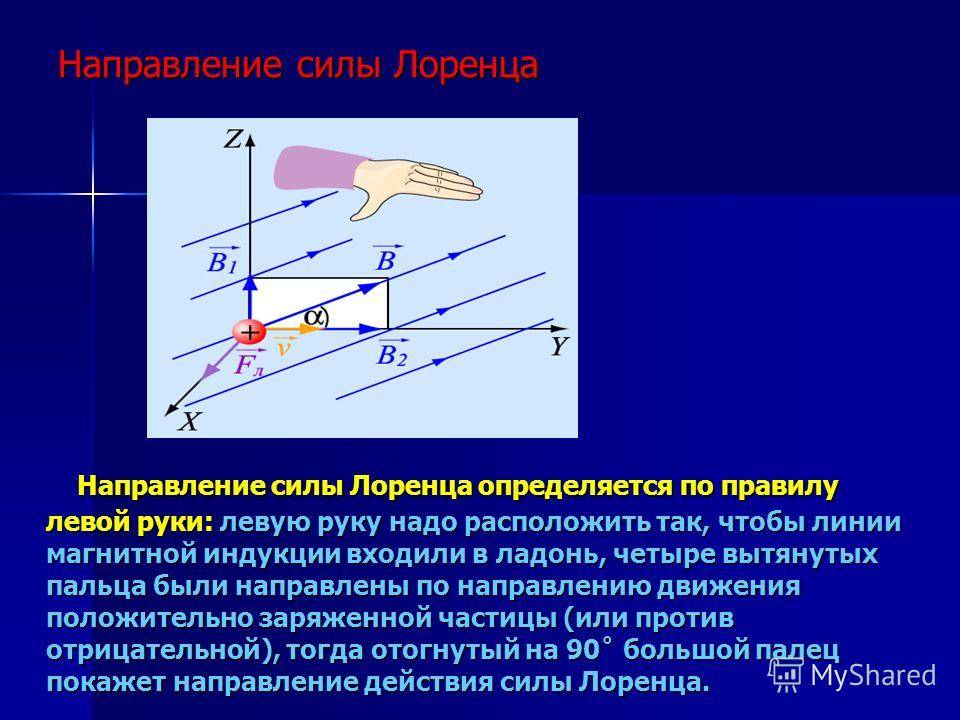
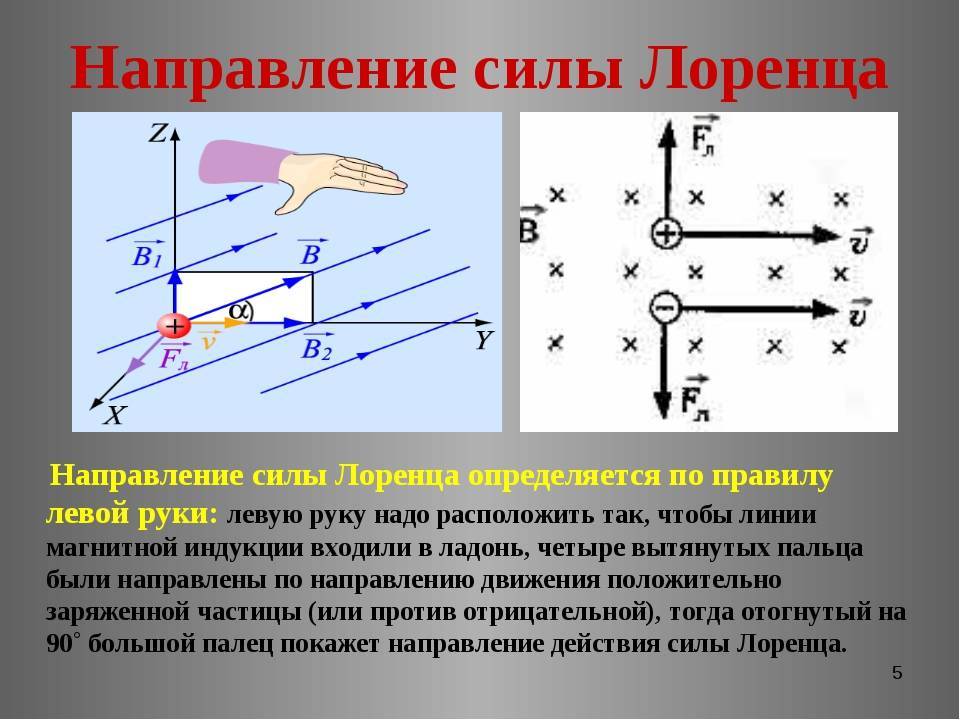
С помощью правила левой руки также определяют и направление силы, действующую на отдельную заряженную частицу, движущуюся в магнитном поле. Для самого простого случая, то есть когда частица движется перпендикулярно линиям магнитного поля, это правило звучит так: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца были направлены по движению положительно заряженной частицы (или против движения отрицательно заряженной), то отставленный на девяносто градусов большой палец покажет направление действующей на частицу силы.

Обратим внимание ещё на один важный момент: магнитное поле не действует в случаях, если прямолинейный проводник с током или скорость движущейся заряженной частицы параллельны линиям магнитного поля или совпадают с ними

Задачи по теме «сила Лоренца»

Даже если вы не новичок, прежде чем решать задачи, прочтите общую памятку и на всякий случай держите под рукой полезные формулы. 

Задача на силу Лоренца №1

Условие 

Электрон с энергией 300 эВ движется перпендикулярно линиям индукции однородного магнитного поля напряженностью 465 А/м. Определить силу Лоренца, скорость и радиус траектории электрона.

Решение

Скорость электрона можно найти из формулы кинетической энергии:

Eк=m·v22v=2Eкm

Сила Лоренца является центростремительной силой, значит, по второму закону Ньютона, можно записать:

Магнитная индукция равна напряженности, умноженной на магнитную постоянную. Подставив ранее найденное выражение для скорости в формулу для радиуса и силы Лоренца, запишем:

R=m2EктqμH=2EктqμHFл=q2EктμH​

Теперь осталось только подставить значения и вычислить:

v=2·4,8·10-169,1·10-31=3,25·107 мсFл=4·3,14·10-7·465·1,6·10-19·3,25·107=3·10-15НR=2·4,8·10-16·9,1·10-314·3,14·10-7·465·1,6·10-19=,32 м

Ответ: v=3,25·107 мс; Fл=3·10-15Н; R=,32 м.

Задача на силу Лоренца №2

Условие

Альфа-частица влетает в магнитное поле с индукцией 1 Тл перпендинулярно силовым линиям. Найти момент импульса частицы относительно центра окружности, по которой она будет двигаться.

Решение

Когда частица влетает в поле перпендикулярно силовым линиям, на нее начинает действовать сила Лоренца, которая выполняет роль центростремительной силы. Радиус окружности, по которой будет двигаться частица:

R=mvQBm=6,65·10-27 кг – масса альфа частицыQ=2e=3,2·10-19Кл – заряд альфа частицы

Момент импульса частицы относительно центра окружности найдем по формуле:

L=mvR=m2v2QB=6,65·10-272·,35·10723,2·10-19·1=5,42·10-21кг·м2с

Ответ: 5,42·10-21 кг·м2с.

Задача на силу Лоренца №3

Условие

В однородном магнитном поле с индукцией  В = 0,5 Тл вращается с частотой n = 10 с-1 стержень длиной l = 20 см. Ось вращения параллельна линиям индукции и проходит через один из концов стержня перпендикулярно его оси. Определите разность потенциалов U на концах стержня.

Решение

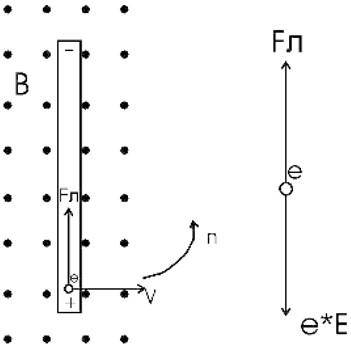
Рассмотрим физическую суть процессов, проходящих в стержне. Когда стержень движется в магнитном поле, в нем возникает ЭДС индукции, которая обусловлена действием силы Лоренца на заряды стержня.

Под действием этой силы в стержне происходит разделение зарядов: свободные электроны перемещаются вверх и между концами стержня возникает разность потенциалов.

Заряды на концах стержня создают поле E, препятствующее дальнейшему разделению зарядов. В какой-то момент сила Лоренца уравновесится с силой возникающего поля:

Fл=e·ЕЕ=Fле=evBe=vB

Скорость нижнего конца стержня, а значит, и скорость электронов в нем, можно найти, зная частоту вращения и длину стержня:

v=2π·n·l

C учетом этого, перепишется выражения для напряженности электрического поля:

 Е=2πnlB

Индуцируемая разность потенциалов, по определению, равна:

U=Е·lU=2πnl2B=2·3,14·10-1·,22·,5=1,3В

Ответ: 1,3 В.

Задача на силу Лоренца №4

Условие

Какая сила действует на заряд 0,005 Кл, движущийся в магнитном поле с индукцие 0,5 Тл со скоростью 150 м/с под углом 45 градусов к вектору магнитной индукции?

Решение

Это простейшая задача на определение силы Лоренца. Вспомним формулу и запишем, что на заряд действует сила Лоренца, равная:

F=q·v·B·sinα

Подставим значения и вычислим:

F=,005·150·,5·22=,26 Н

Ответ: 0,26 Н.

Задача на силу Лоренца №5

Условие

На тело с зарядом 0,8 мКл, движущееся в магнитном поле, со стороны поля действует сила, равная 32Н. Какова скорость тела, если вектор магнитного поля перпендикулярен ей?

Решение

Это классическая задача на применение формулы силы Лоренца. Так как векторы скорости и магнитной индукции перпендикулярны, можно записать:

F=qvBsinα=qvBv=FqB=32,8·10-3·2=20·103 мс

Ответ: 20000 м/с.

Проходите магнитостатику? Вам также может быть интересно:

1. Задачи на закон Био-Савара-Лапласа.
2. Задачи на теорему о циркуляции магнитного поля.

Главное правило

Рассмотренный нами пример является частным случаем алгоритма буравчика. Существует несколько вариантов формулировок правила, применяемых в различных ситуациях.

Общая, или главная формулировка, позволяет распространить данное правило на все случаи. Это вариант мнемонического правила, используемый для определения ориентации результирующей векторного произведения, называемого аксиальным вектором, а также для выбора связанного с этими векторами правого базиса (трёхмерной системы координат), что позволяет определить знак аксиального вектора.

Главное правило позволяет определить направление в пространстве аксиальных векторов, важных для вычислений:

• угловой скорости;
• параметров индукционного тока;
• магнитной индукции.

Хотя ориентация аксиального вектора является условной, она важна для расчётов: придерживаясь принятого алгоритма выбора, легче производить вычисления, без риска перепутать знаки.

Во многих случаях применяют специальные формулировки, хорошо описывающие частные случаи в конкретной ситуации.

Действие магнитного поля на ток. Правило левой руки.

Поместим между полюсами магнита проводник, по кото­рому протекает постоянный электрический ток. Мы тотчас же заметим, что проводник будет выталкиваться полем магнита из междуполюсного пространства.

Объяснить это можно следующим образом. Вокруг провод­ника с током (Рисунок 1.) образуется собственное магнитное поле, силовые линии которого по одну сторону проводника направ­лены так же, как и силовые линии магнита, а по другую сто­рону проводника — в противопо­ложную сторону. Вследствие это­го с одной стороны проводника (на рисунке 1 сверху) маг­нитное поле оказывается сгущен­ным, а с другой его стороны (на рисунке 1 снизу) — разрежен­ным. Поэтому проводник испыты­вает силу, давящую на него вниз. И если проводник не закреплен, то он будет перемещаться.

Рисунок 1. Действие магнитного поля на ток.

Правило левой руки

Для быстрого определения направления движения провод­ника с током в, магнитном поле существует так называемое правило левой руки (рисунок 2.).

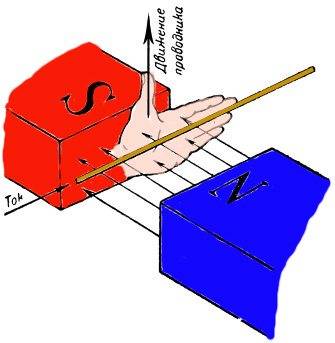
Рисунок 2. Правило левой руки.

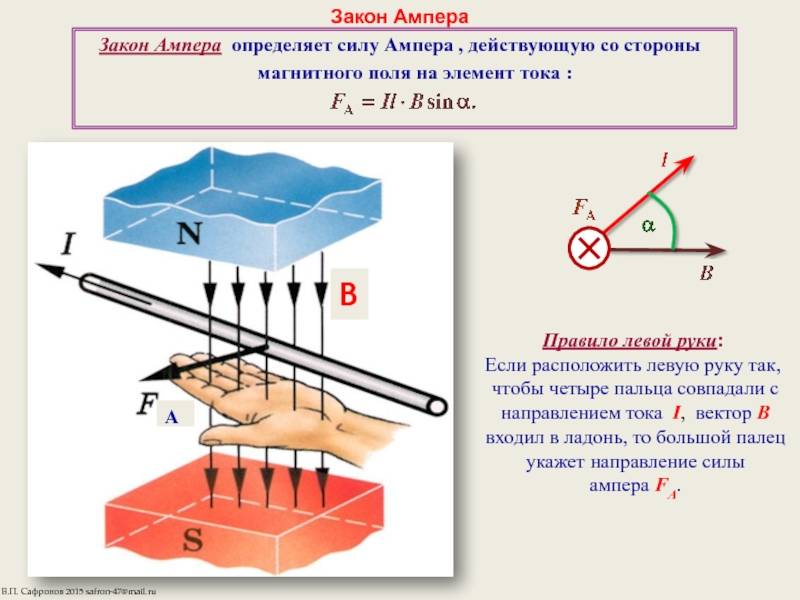
Правило левой руки состоит в следую­щем: если поместить левую руку между полюсами маг­нита так, чтобы магнитные силовые линии входили в ладонь, а четыре пальца ру­ки совпадали с направлением тока в проводнике, то боль­шой палец покажет направ­ление движения проводника.

Итак, на проводник, по которому протекает электри­ческий ток, действует сила, стремящаяся перемещать его перпендикулярно магнитным силовым линиям. Опытным путем можно определить величину этой силы. Оказы­вается, что сила, с которой магнитное поле действует на проводник с током, прямо пропорциональна силе тока в проводнике и длине той части проводника, которая нахо­дится в магнитном поле (рисунок 3 слева).

Это правило справедливо, если проводник расположен под прямым углом к магнитным силовым линиям.

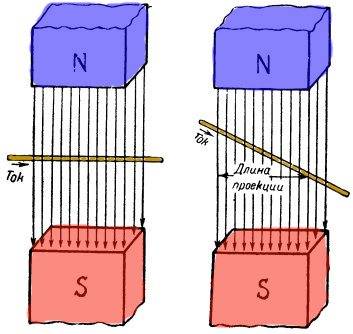
Рисунок 3. Сила взаимодействия магнитного поля и тока.

Если же проводник расположен не под прямым углом к магнитным силовым линиям, а, например, так, как изобра­жено на рисунке 3 справо, то сила, действующая на проводник, будет пропорциональна силе тока в проводнике и длине проекции части проводника, находящейся в магнитном поле, на плос­кость, перпендикулярную магнитным силовым ли­ниям. Отсюда следует, что если проводник паралле­лен магнитным силовым линиям, то сила, дейст­вующая на него, равна нулю. Если же проводник перпендикулярен направ­лению магнитных силовых линий, то сила, действую­щая на него, достигает наибольшей величины.

Сила, действующая на проводник с током, зави­сит еще и от магнитной индукции. Чем гуще рас­положены магнитные си­ловые линии, тем больше сила, действующая на проводник с током.

Подводя итог всему изложенному выше, мы можем действие магнитного поля на проводник с током выразить следующим правилом:

Сила, действующая на проводник с током, прямо пропорциональна магнитной индукции, силе тока в проводнике и длине проекции части проводника, находящейся в магнитном поле, на плоскость, перпендикулярную маг­нитному потоку.

Необходимо отметить, что действие магнитного поля на ток не зависит ни от вещества проводника, ни от его сечения. Дей­ствие магнитного поля на ток можно наблюдать даже при от­сутствии проводника, пропуская, например, между полюсами магнита поток быстро несущихся электронов.

Действие магнитного поля на ток широко используется в науке и технике. На использовании этого действия основано устройство электродвигателей, превращающих электрическую энергию в механическую, устройство магнитоэлектрических приборов для измерения напряжения и силы тока, электроди­намических громкоговорителей, превращающих электрические колебания в звук, специальных радиоламп — магнетронов, катодно-лучевых трубок и т. д. Действием магнитного поля на ток пользуются для измерения массы и заряда электрона и даже для изучения строения вещества.

Похожие материалы:

• Магнитное поле тока. Магнитные силовые линии
• Напряженность магнитного поля
• Магнитная индукция
• Электромагнитная индукция
• Правило правой руки
• Взаимоиндукция
• Самоиндукция
• ЭДС самоиндукции: основные послулаты
• Постоянные магниты

Комментарии

Громова Ева 27.02.2018 18:58 Спасибо большое за статью!

Цитировать

асаев антон 04.09.2014 04:56 спасибо создателю сайта

Цитировать

Обновить список комментариев

Что такое сила Лоренца — определение, когда возникает, получение формулы

Известно, что электрический ток – это упорядоченное перемещение заряженных частиц. Установлено также, что во время движения в магнитном поле каждая из этих частиц подвергается действию силы. Для возникновении силы требуется, чтобы частица находилась в движении.

Сила Лоренца – это сила, которая действует на электрически заряженную частицу при её движении в магнитном поле. Её направление ортогонально плоскости, в которой лежат векторы скорости частицы и напряженности магнитного поля. Равнодействующая сил Лоренца и есть сила Ампера. Зная ее, можно вывести формулу для силы Лоренца.

Время, требуемое для прохождения частицей отрезка проводника, , где – длина отрезка, – скорость частицы. Суммарный заряд, перенесенный за это время через поперечное сечение проводника, . Подставив сюда значение времени из предыдущего равенства, имеем

                             (2)

В то же время , где – количество частиц, находящееся в рассматриваемом проводнике. При этом , где – заряд одной частицы. Подставив в формулу значение из (2), можно получить:

Таким образом,

Используя (1), предыдущее выражение можно записать как

После сокращений и переносов появляется формула для вычисления силы Лоренца

С учетом того, что формула записана для модуля силы, ее необходимо записать так:

                            (3)

Поскольку , то для вычисления модуля силы Лоренца неважно, куда направлена скорость, – по направлению силы тока или против, – и можно сказать, что – это угол, образуемый векторами скорости частицы и магнитной индукции. Запись формулы в векторном виде будет выглядеть следующим образом:

Запись формулы в векторном виде будет выглядеть следующим образом:

– это векторное произведение, результатом которого является вектор с модулем, равным .

Исходя из формулы (3), можно сделать вывод о том, что сила Лоренца является максимальной в случае перпендикулярности направлений электрического тока и магнитного поля, то есть при , и исчезать при их параллельности ().

Необходимо помнить, что для получения правильного количественного ответа – например, при решении задач, – следует пользоваться единицами системы СИ, в которой магнитная индукция измеряется в теслах (1 Тл = 1 кг·с−2·А−1), сила – в ньютонах (1 Н = 1 кг·м/с2), сила тока – в амперах, заряд в кулонах (1 Кл = 1 А·с), длина – в метрах, скорость – в м/с.

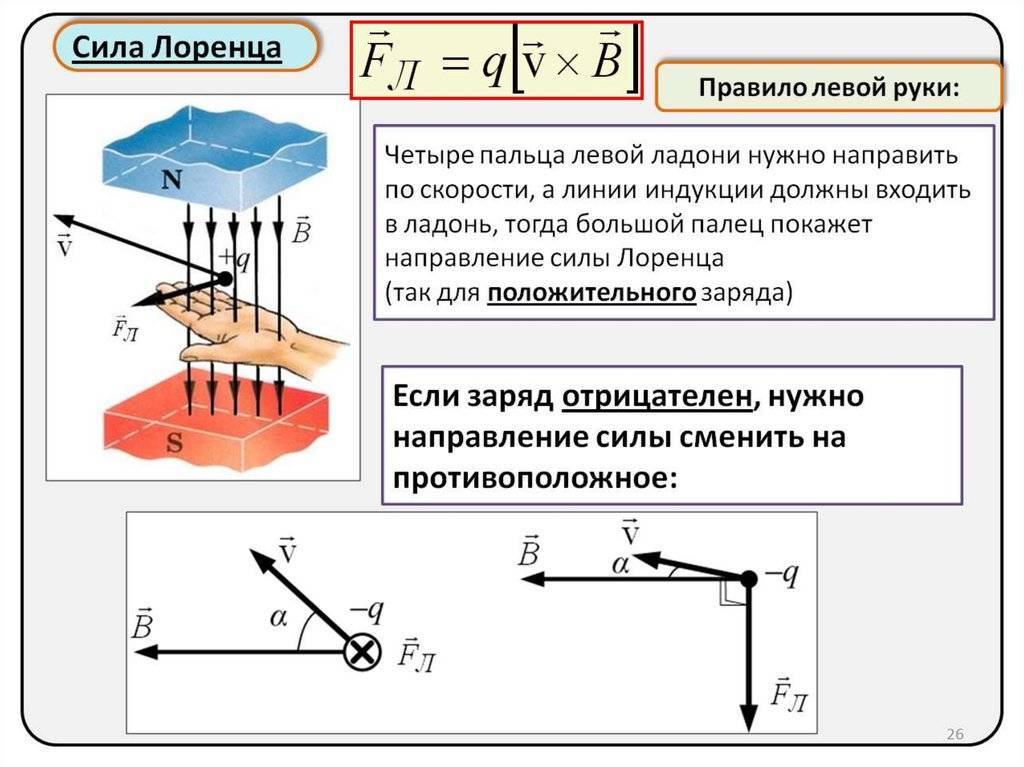
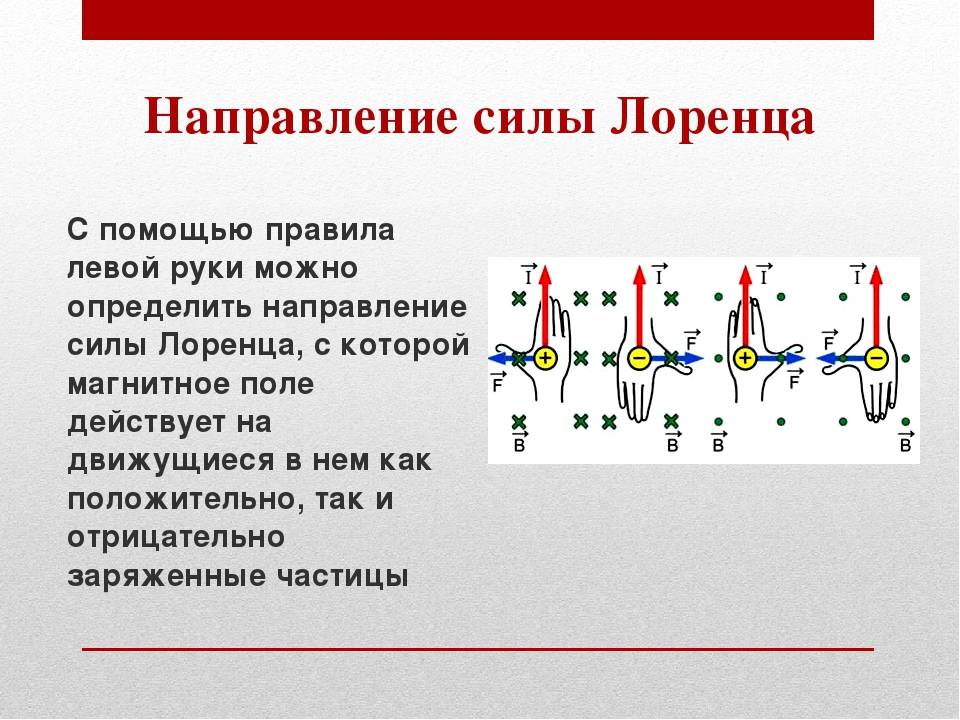
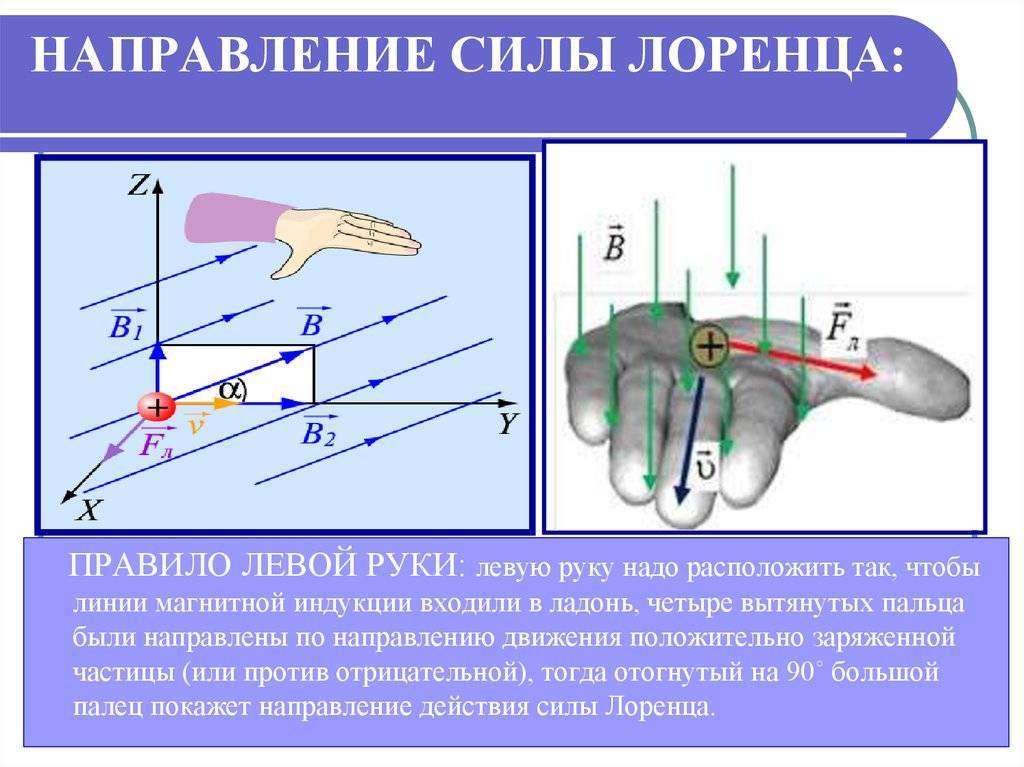
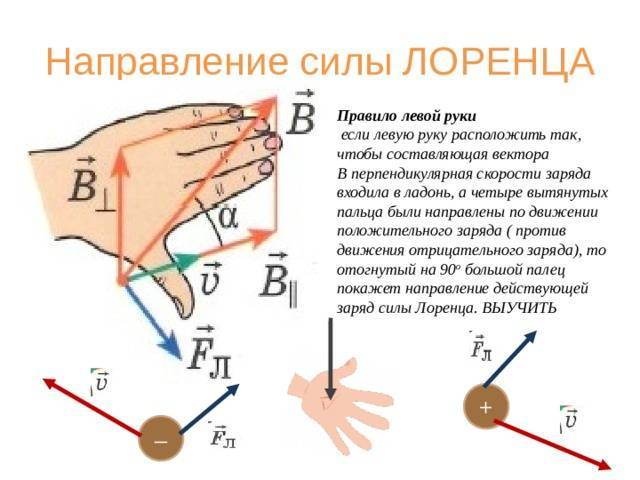
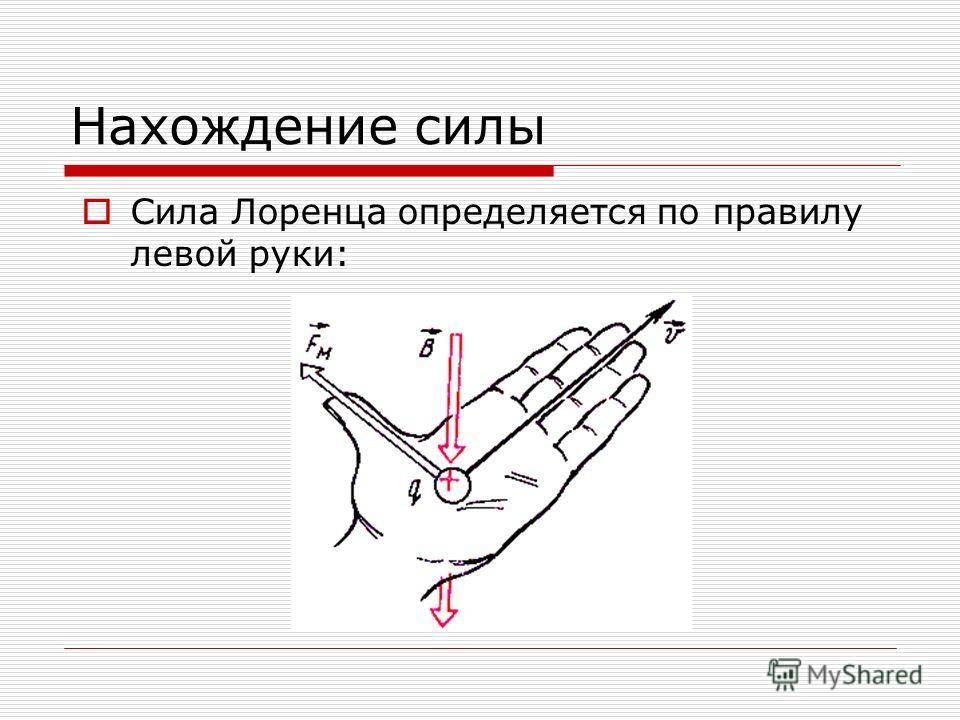
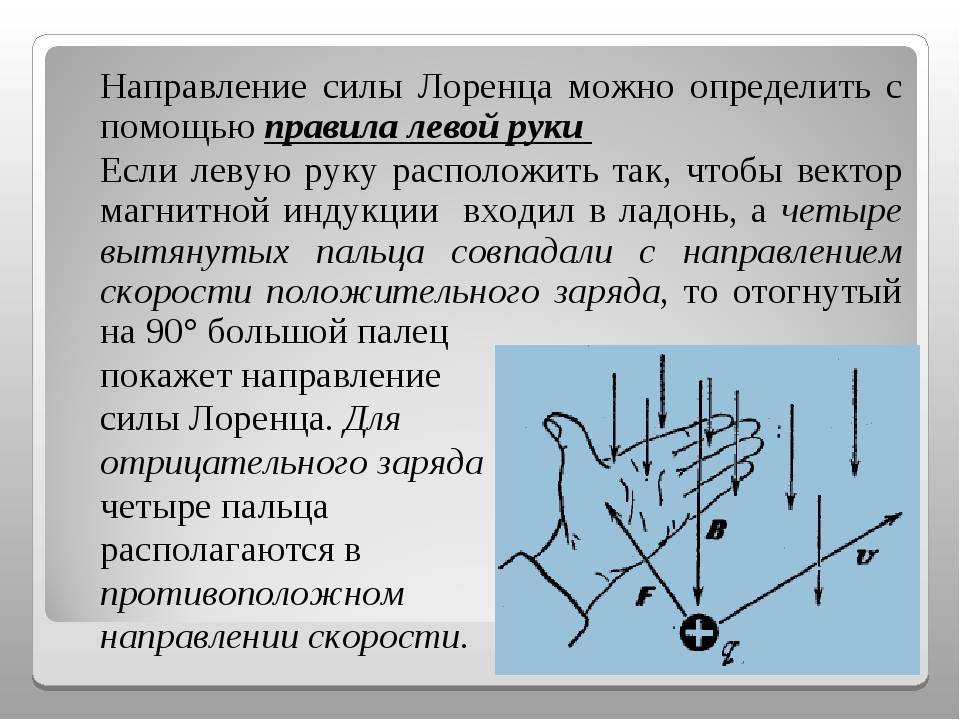
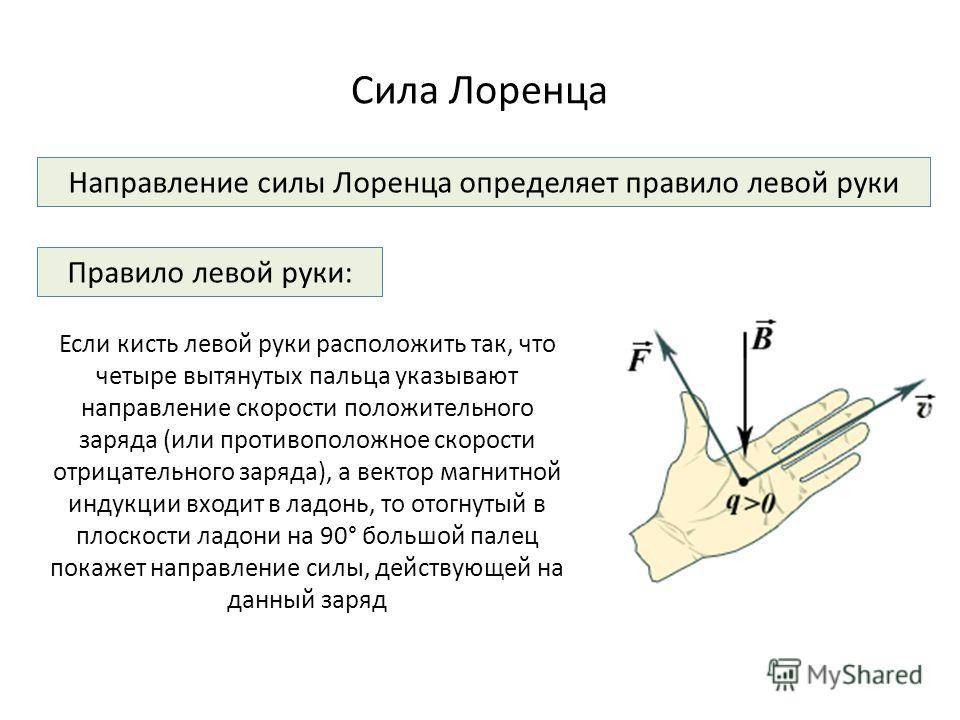
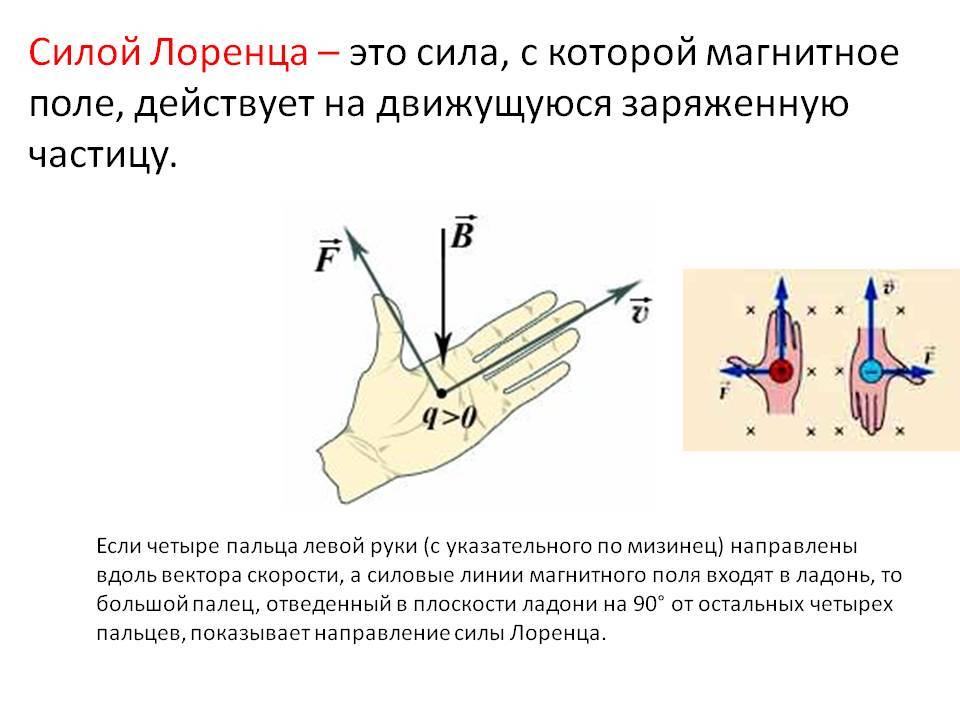
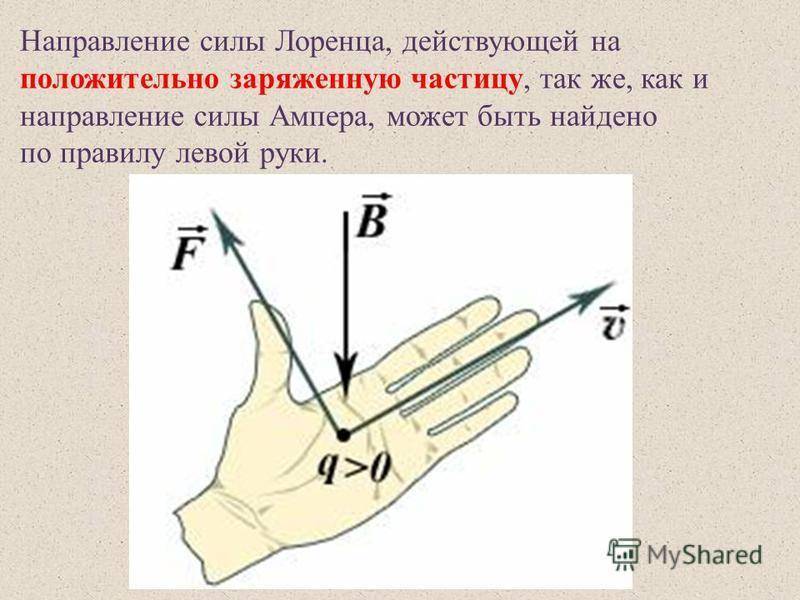
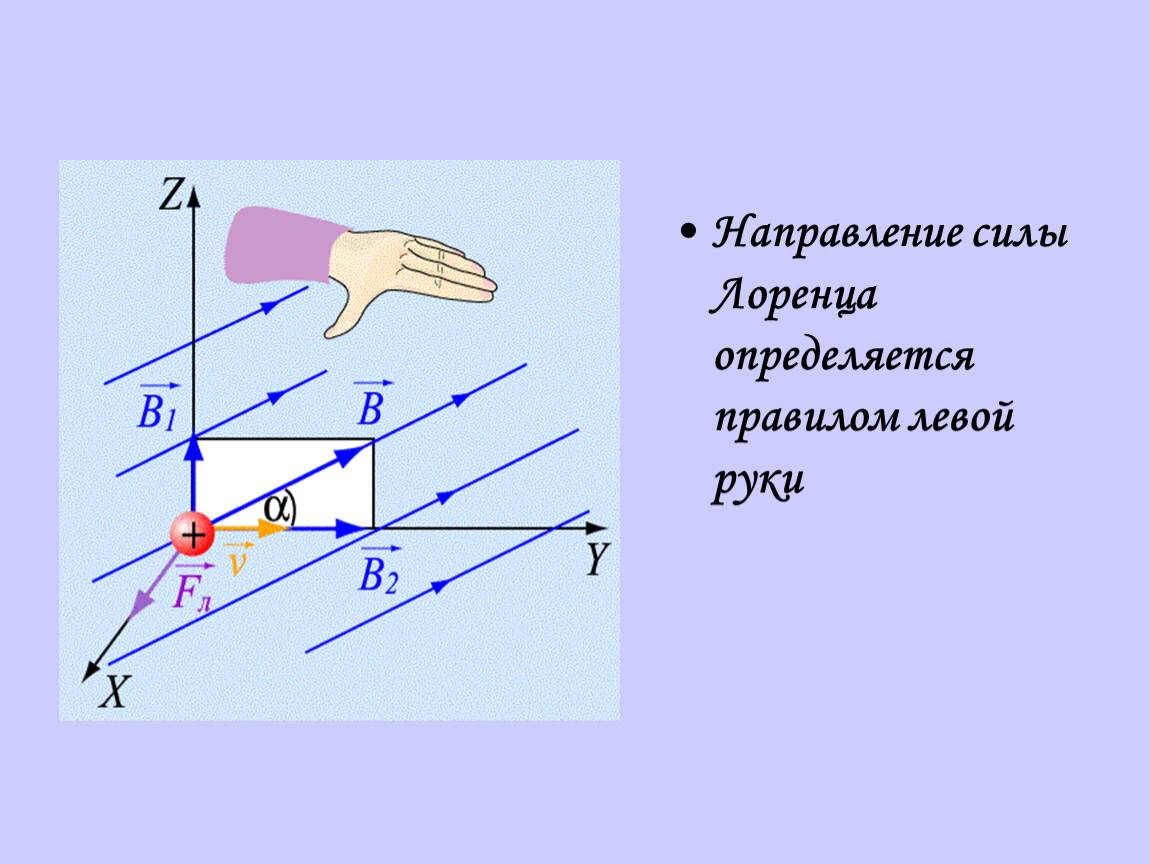
Определение направления силы Лоренца с помощью правила левой руки

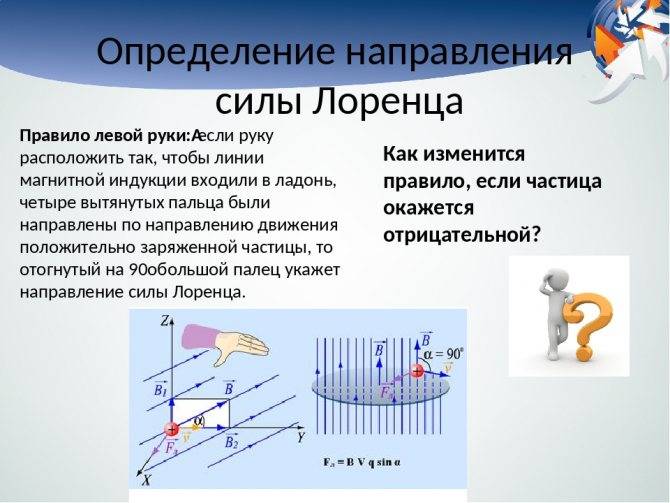
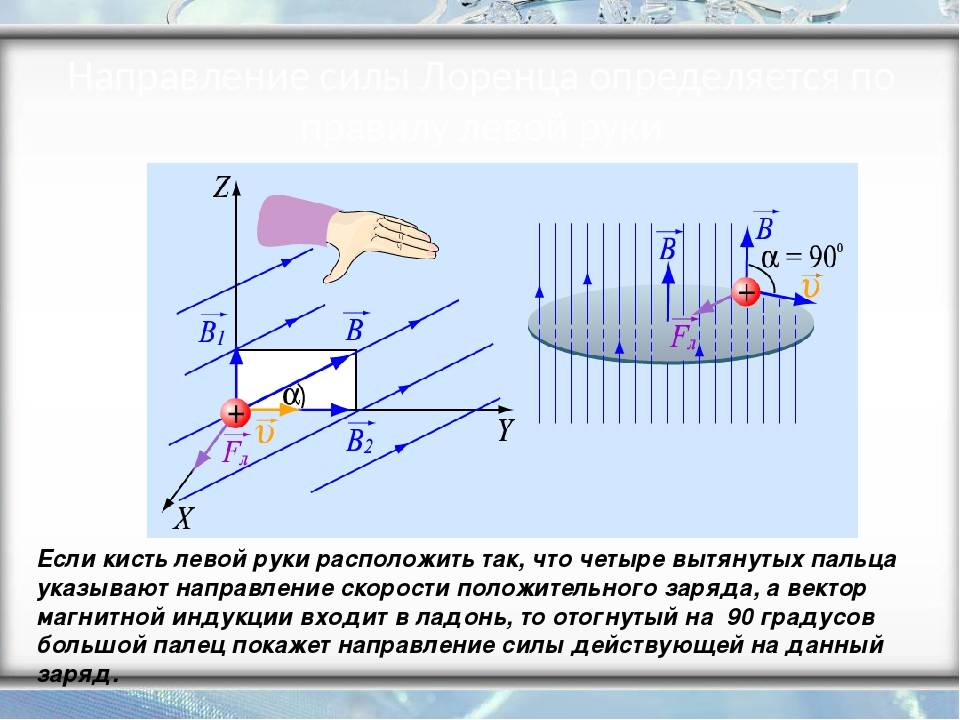
Поскольку в мире макрообъектов сила Лоренца проявляется как сила Ампера, для определения ее направления можно пользоваться правилом левой руки.

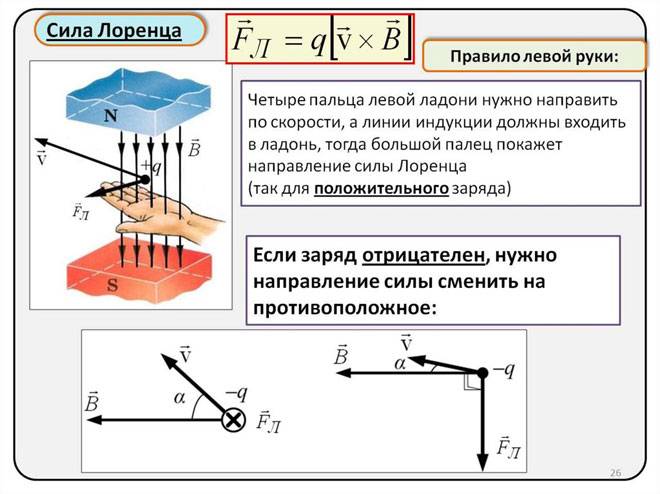
Нужно поставить левую руку так, чтобы раскрытая ладонь находилась перпендикулярно и навстречу линиям магнитного поля, четыре пальца следует вытянуть в направлении силы тока, тогда сила Лоренца будет направлена туда, куда указывает большой палец, который должен быть отогнут.

Движение заряженной частицы в магнитном поле

В простейшем случае, то есть при ортогональности векторов магнитной индукции и скорости частицы сила Лоренца, будучи перпендикулярной к вектору скорости, может менять только её направление. Величина скорости, следовательно, и энергия будут оставаться неизменными. Значит, сила Лоренца действует по аналогии с центростремительной силой в механике, и частица перемещается по окружности.

В соответствии со II законом Ньютона () можно определить радиус вращения частицы:

.

Необходимо обратить внимание, что с изменением удельного заряда частицы () меняется и радиус. При этом период вращения T = =

Он не зависит от скорости, значит, взаимное положение частиц с различными скоростями будет неизменным

При этом период вращения T = = . Он не зависит от скорости, значит, взаимное положение частиц с различными скоростями будет неизменным.

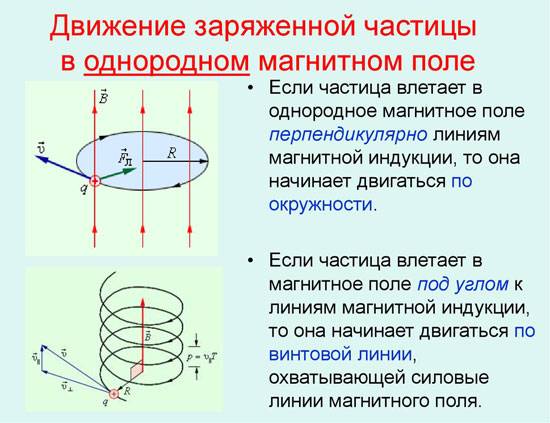
В более сложном случае, когда угол между скоростью частицы и напряженностью магнитного поля является произвольным, она будет перемещаться по винтовой траектории – поступательно за счет составляющей скорости, направленной параллельно полю, и по окружности под влиянием ее перпендикулярной составляющей.