Параллельное и последовательное соединение проводников

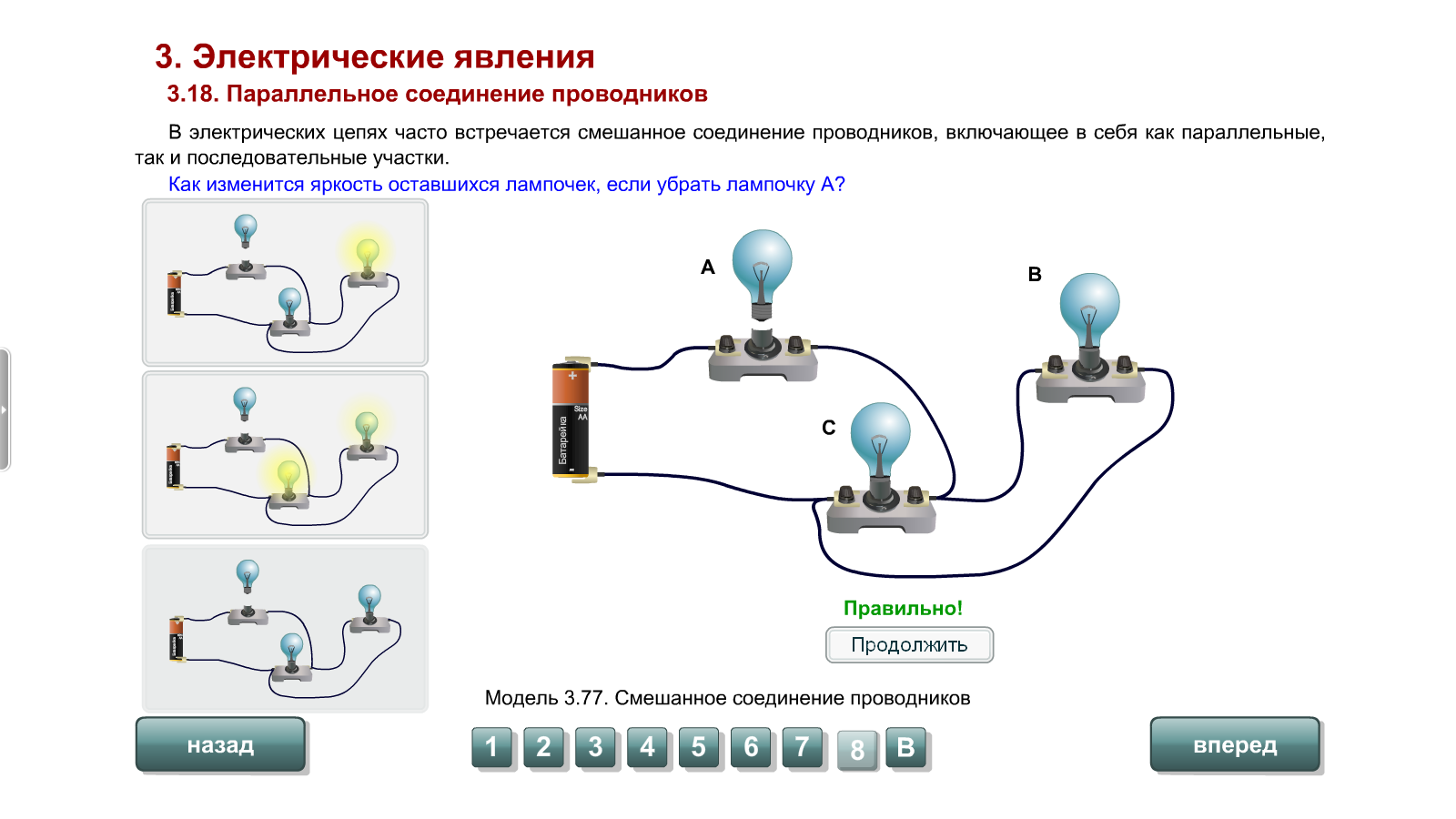
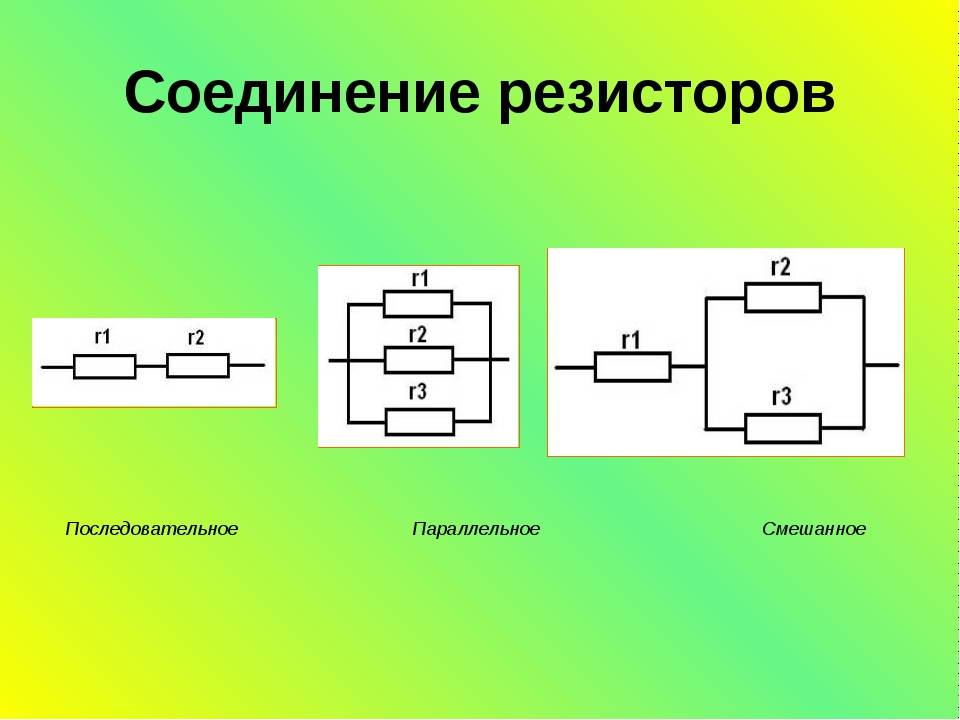
Ток в цепи параллельно соединенных резисторов

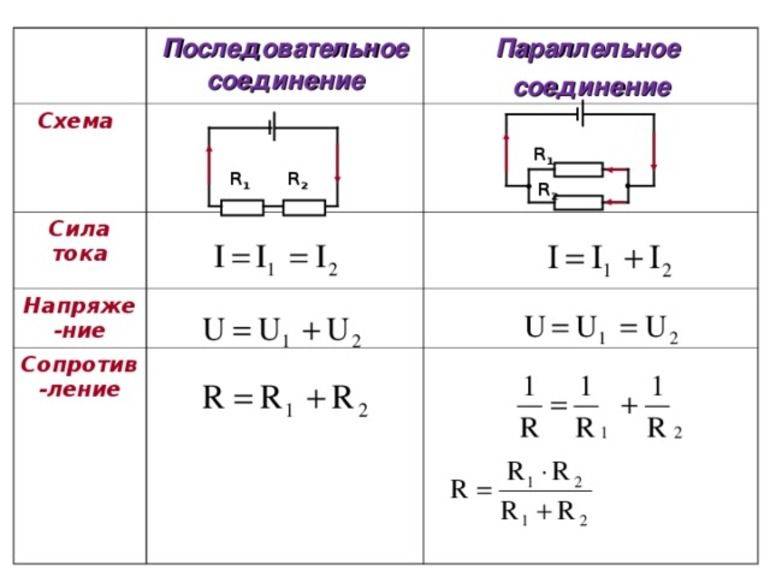
В ходе рассмотрения соответствующих участков разветвленных схем необходимо помнить о равенстве токов на входе и выходе из каждого узла, а также до и после группы из параллельных резисторов. Это правило поможет проверить правильность расчетов. Если отмеченное соответствие не соблюдено, устраняют ошибку вычислений.

Сила тока при параллельном соединении

С применением рассмотренных выше исходных данных для двух сложных схем можно сделать расчет для каждой отдельной ветки.

Пример 1:

• общий ток в цепи составляет 0,8 А;
• распределение напряжений на отдельных участках несложно определить по рассчитанным эквивалентным сопротивлениям: U12 = I * Rэкв1 = 0,8 * (2*4)/ (2+4) = 0,8 * 1,3 = 1,04 V;
• по стандартному алгоритму вычисляют значения токов: I1 = U12/R1 = 0,52 А, I2 = U12/R2 = 0,26 А;
• суммированием проверяют корректность вычислений: I = I1 + I2 = 0,52 + 0,26 ≈ 0,8 А.

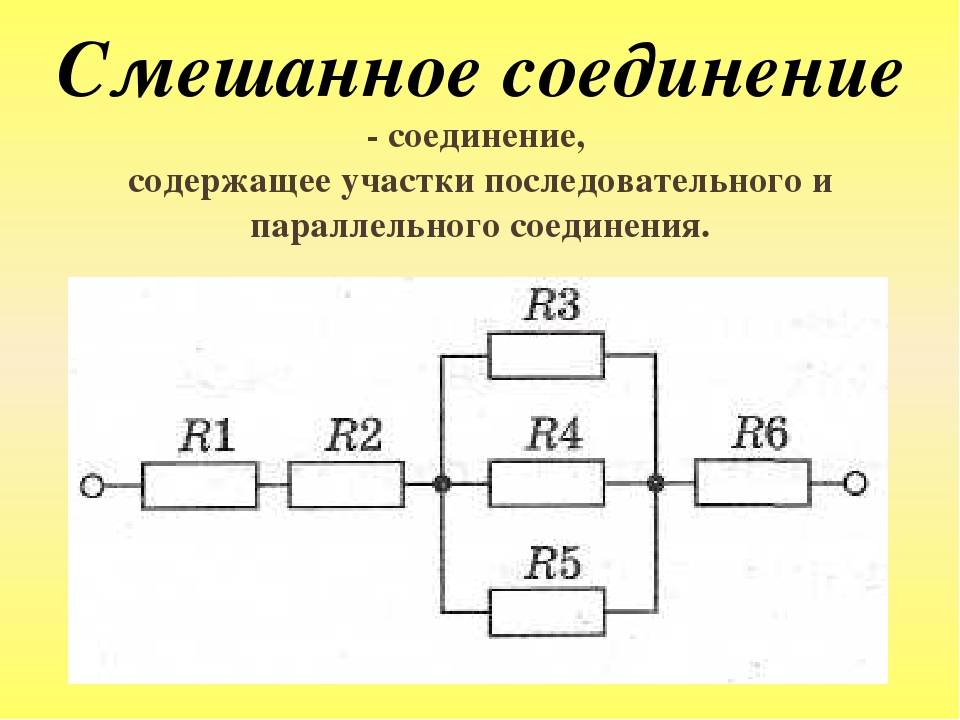
Пример 2 (смешанный способ соединения резисторов):

• ток в этом варианте – 1,2 А;
• напряжение на участке с группой параллельных резисторов составляет Uав = I * Rэкв(12345) = 1,2*2,5 =3V;
• по аналогии с предыдущим примером несложно вычислить ток в каждой отдельной ветке: I12 = Uав/(R1 + R2) = 3/ (15 + 5) = 0,15 А;
• I3 = Uав/ R3 = 3/ 5 = 0,6 А;
• I4 = Uав/ R4 = 3/ 10 = 0,3 А;
• I5 = Uав/ R5 = 3/20 = 0,15 А;
• по правилу равенства токов на входе и выходе из узла проверяют правильность сделанных расчетов: I = I12 + I3 + I4 + I5 = 0,15 + 0,6 + 0,3 + 0,15 = 1,2 А.

Мощность при параллельном соединении

Для правильного выбора резистивных компонентов электрических цепей обязательно следует учитывать мощность рассеивания. Этот параметр (Р) рассчитывают по классической формуле P = U (напряжение на выводах, В) * I (сила тока в цепи, А). Он косвенно определяет энергию, которая расходуется на выделение тепла. Также применяют пропорции:

P = I2 *R = U2/ R.

К сведению. Конструкция каждого элемента рассчитана на определенный рабочий температурный диапазон. Превышение порога способно разрушить деталь, место пайки, соседние компоненты. Следует не забывать об одновременном существенном изменении сопротивления, которое способно нарушить функциональное состояние электрической схемы.

Для расчета выбирают подходящую формулу с учетом известных исходных параметров (данные из примера 2 в предыдущем разделе):

• ток – 1,2 А;
• на сопротивлении R6=7,5 Ом мощность рассеивания составит: P6 = I2 *R = 1,44 * 7,5 = 10,8 Вт;
• найти такой резистор сложно, так как в стандартном ряду предлагаются номиналы от 0,05 до 5Вт;
• в другой цепи (R5=20 Ом) расчетный ток составит 0,15 А, поэтому P5= 0,0225 * 20 = 0,45 Вт;
• в этом случае можно выбрать изделие с подходящей мощностью рассеивания в стандартной номенклатуре 0,5 Вт (специалисты рекомендуют делать 1,52 кратный запас, поэтому лучше использовать резистор на 1 Вт).

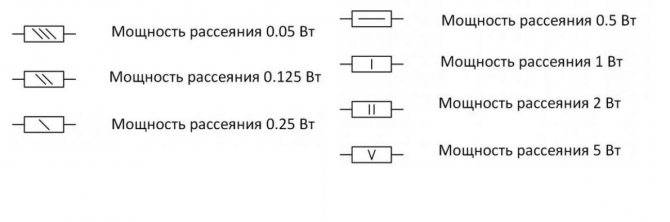
Стандартные обозначения на электрических схемах и типовые номиналы по мощности

К сведению. При выборе резисторов следует учитывать класс изделия по точности электрического сопротивления. В серийных деталях допустимы отклонения 5-20%.

Как найти сопротивление при параллельном соединении

Для расчета этого параметра применяют формулы:

• 1/G;
• U/I;
• U2/P;
• P/I2.

Выбирают подходящий вариант (комбинацию) с учетом имеющихся исходных данных. Следует помнить о едином напряжении на входе и выходе и разных токах в отдельных ветках. Технология вычислений рассмотрена в предыдущих разделах.

Параллельное соединение

Необходимость в параллельном включении возникает в случае, когда напряжения источника питания недостаточно для запитки нескольких последовательно соединённых светодиодов. Теоретически, в самом простом варианте можно было бы отдельно объединить все аноды и все катоды излучающих диодов. После чего подключить их к источнику напряжения с соблюдением полярности. Нотакая схема не работоспособна, так как дифференциальное сопротивление открытого светодиода чрезмерно мало, что провоцирует режим короткого замыкания. В результате все светодиоды в цепи единожды вспыхнут и навсегда погаснут. Но как говорят: «Правило без исключений не бывает». В китайских игрушках и зажигалках с подсветкой можно увидеть, что светодиоды запитаны прямо от батареек без каких-либо промежуточных элементов. Почему они не перегорают? Дело в том, что ток в цепи ограничен внутренним сопротивлением круглых батареек типа AG1. Их мощности недостаточно, чтобы нанести вред светодиоду.

Ограничить резкое нарастание тока в нагрузке можно с помощью резистора. О том, как это грамотно сделать с одним светодиодом, подробно написано в данной статье. Для цепи из нескольких параллельно подключенных LED с одним резистором схема примет следующий вид.

Нои этот вариант не пригоден для конструирования осветительных устройств с высокой надёжностью. Почему? Ответ на этот вопрос кроется в особенностях строения полупроводников. В процессе производства полупроводниковых элементов невозможно получить два абсолютно одинаковых прибора. Даже у светодиодов из одной партии будет разное дифференциальное (внутреннее) сопротивление, от которого зависит величина прямого напряжения. Это касается не только светодиодов, но и других полупроводников. Среди диодов, транзисторов и тиристоров тоже не найти двух приборов с равными электрическими параметрами. Из второй схемы видно, что резистор R1 ограничивает только суммарный ток цепи, который затем распределяется по ветвям со светодиодами в зависимости от их сопротивления. По закону Ома светодиод с наименьшим сопротивлением p-n-перехода получит наибольшую порцию тока. И скорее всего он будет больше номинального значения, что ускорит деградацию кристалла. Работа светодиода в режиме перегрузки по току рано или поздно приведёт к выходу из строя на обрыв. Оставшиеся в работе светодиоды распределят между собой ток сгоревшего элемента, что также приведёт к резкой потере яркости.

Ниже приведен единственно верный вариант параллельного включения светодиодов.

Здесь последовательно с каждым светодиодом подключен ограничительный резистор. Такое схемотехническое решение позволяет выровнять токи в каждой отдельной ветви, не позволяя им превышать рабочее значение.

Пример расчета

Для закрепления теоретических знаний параллельное соединение светодиодов рассмотрим на конкретном примере.

В схеме включены два светодиода: слаботочный красный и мощный одноваттный белый, которые для удобства можно запитать от разных выключателей.

Дано:

• источник напряжения U = +5 В;
• LED1 – красного свечения с ULED1 = 1,8 В и ILED1 = 0,02 А;
• LED2 – белого свечения с ULED2 = 3,2 В и ILED2 = 0,35 А.

Требуется рассчитать параметры и выбрать резисторы R1 и R2.

При параллельном включении к обеим ветвям (R1-LED1 и R2- LED2) прикладывается одинаковое напряжение, равное 5 В. Сопротивление каждого резистора определим по формуле:

Округляем полученное значение R2 до ближайшего большего значения из стандартного ряда E24 – 5,1 Ом. Подставив его обратно в формулу, находим реальный ток во второй ветви: С учетом возможного отклонения сопротивления выбранного резистора, которое для ряда Е24 может достигать 5%, ток 0,33 А является оптимальным. Снижение рабочего тока примерно на 4% сильно не повлияет на яркость, но позволит светодиоду работать без перегрузок.

Мощность, которую должны рассеивать резисторы, определим с учетом пересчёта тока LED2 по формуле:

Резистор R1 подойдёт любой как планарный, так и с выводами сопротивлением 160 Ом и мощностью 0,125 Вт. Корпус резистора R2 должен эффективно отводить тепло в течение длительной работы светильника. Поэтому его выбираем с двойным запасом по мощности, а именно: 5,1 Ом – 1 Вт.

Преобразование треугольника в эквивалентную звезду

Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи

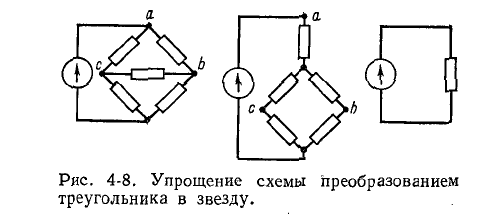
сохраняются неизменными. Иначе говоря, эквивалентность треугольника и звезды понимается в том смысле, что при одинаковых напряжениях между одноименными выводами токи, входящие в одноименные выводы, одинаковы. Это равносильно тому, что мощности в этих цепях одинаковы.

На рис. 4-8 показан случай, когда преобразование треугольника в эквивалентную звезду дает возможность преобразовать многоконтурную схему в одноконтурную.

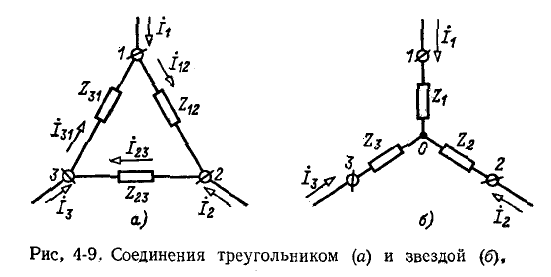
Для вывода расчетных выражений, служащих для преобразования треугольника в эквивалентную звезду, ниже приняты следующие обозначения (рис. 4-9):

• — сопротивления сторон треугольника;
• — сопротивления лучей звезды;
• — токи, подходящие к выводам 1, 2, 3\
• — Токи в ветвях треугольника.

Выразим токи в ветвях треугольника через приходящие токи.

По второму закону Кирхгофа сумма напряжений в контуре треугольника равна нулю:

По первому закону Кирхгофа для узлов 2 и 1

Решение этих уравнений относительно Дает:

Напряжение между выводами 1 и 2 схемы рис. 4-9, а будет:

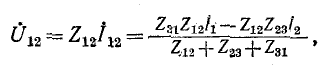
a в схеме рис. 4-9, б оно равно:
Для эквивалентности необходимо равенство напряжений при всяких токах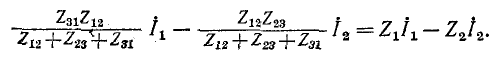

Это возможно при условии:

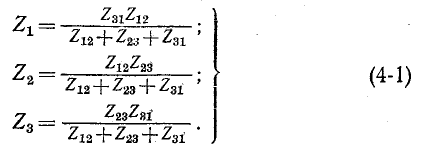
Третье выражение получается в результате круговой замены индексов.

Итак, комплексное сопротивление луча звезды равно произведению комплексных сопротивлений прилегающих сторон треугольника, деленному на сумму комплексных сопротивлений трех сторон треугольника.

Выше было получено выражение для тока в стороне 1—2 треугольника в зависимости от токов Круговой заменой индексов можно получить токи в двух других сторонах треугольника:

 

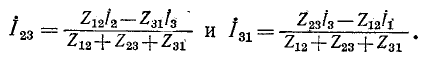
Параллельное подключение

Этот тип подсоединения предполагает установку проводников в общих начальных и конечных точках. В результате нагрузки монтируются параллельно, а их количество может быть любым. Для исследования главных свойств такой электроцепи необходимо собрать простую схему, состоящую из источника питания, выключателя и двух ламп. Ко всем нагрузкам также необходимо подключить по амперметру. Еще один прибор этого типа предназначен для измерения показателя общего сопротивления.

Если замкнуть ключ, то измерительные приборы, подсоединенные к нагрузке, покажут значение токовой нагрузки I1 и I2. На общем амперметре в такой ситуации можно будет увидеть суммарное значение токов на каждом из двух участков схемы. Это существенно отличает параллельное соединение от последовательного. В случае если одна нагрузка выходит из строя, то остальные продолжат свою работу. Именно поэтому в бытовых электросетях используется параллельное подсоединение.

Благодаря применению аналогичной схемы, появится возможность определить напряжение при параллельном соединении. Для этого нужно добавить в нее еще один прибор — вольтметр. Полученный с его помощью результат измерения будет общим для любого участка схемы. После этого можно провести расчет параллельного соединения резисторов. Чтобы решить такую задачу, нужно применить закон Ома. Он гласит, что сила тока равна отношению напряжения к сопротивлению.

Это позволяет вывести следующую формулу — U/R = U1/R1 + U2/R2. В ней R и U — показатели суммарного сопротивления и напряжения электроцепи соответственно. U1, U2, R1 и R2 — значения напряжения и сопротивления на первом и втором потребителе. Так как электроток одинаков для всей схемы, то формула для определения сопротивление при параллельном соединении примет вид — 1/R = 1/R1 + 1/R2.

Это говорит о том, что при этом виде подсоединения потребителей сопротивление имеет невысокое значение. Следовательно, токовая нагрузка тока существенно увеличится.

Задачи на конденсаторы и электроемкость с решением

Если вы не знаете, как решать задачи с конденсаторами, сначала посмотрите теорию и вспомните про памятку по решению задач по физике и полезные формулы.

Задача №1 на электроемкость батареи конденсаторов

Условие

Плоский конденсатор емкостью 16 мкФ разрезают на 4 равные части вдоль плоскостей, перпендикулярных обкладкам. Полученные конденсаторы соединяют последовательно. Чему равна емкость батaреи конденсаторов?

Решение

Из условия следует, что площадь получившихся конденсаторов в 4 раза меньше, чем у исходного. Зная это, можно найти емкость каждого полученного конденсатора:

Соединяя 4 таких конденсатора последовательно, получаем:

Ответ: 1 мкФ.

Задача №2 на энергию плоского конденсатора

Условие

Плоский конденсатор заполнили диэлектриком с диэлектрической проницаемостью, равной 2. Энергия конденсатора без диэлектрика равна 20 мкДж. Чему равна энергия конденсатора после заполнения диэлектриком? Считать, что источник питания отключен от конденсатора.

Решение

Энергия конденсатора до заполнения диэлектриком равна:

После заполнения емкость конденсатора изменится:

Энергия конденсатора после заполнения:

Ответ: 40 мкФ.

Задача №3 на последовательное и параллельное соединение конденсаторов

Условие

На рисунке изображена батарея конденсаторов. Каждый конденсатор имеет емкость 1 мкФ. Найдите емкость батареи.

Решение

Как видим, часть конденсаторов соединена параллельно, а часть последовательно. Это типичный пример смешанного соединения конденсаторов. Алгоритм решения задач при смешанном соединении конденсаторов сводится к тому, чтобы упростить схему и свести все только к параллельному или последовательному соединению.

Конденсаторы 3 и 4 соединены параллельно. Складывая их емкость, получаем в итоге последовательное соединение четырех конденсаторов: 1, 2, 5 и 3-4. Для параллельного соединения:

Для последовательного соединения:

Ответ: 0,285 мкФ.

Задача №4 на пролет частицы в конденсаторе

Заряд конденсатора равен 0,3 нКл, а емкость – 10 пФ. Какую скорость приобретет электрон, пролетая в конденсаторе от одной пластины к другой. Начальная скорость электрона равна нулю. 

Решение

По закону сохранения энергии, разность кинетических энергий электрона в начале и в конце пути будет равна работе поля по его перемещению. По условию, начальная кинетическая энергия электрона равна 0. Запишем:

С учетом этого, получим:

Ответ: 10^7 м/с.

Задача №5 на вычисление энергии электрического поля конденсатора

Условие

Конденсатор подключен к источнику постоянного напряжения U=1 кВ. Емкость конденсатора равна 5 пФ. Как изменяться заряд на обкладках конденсатора и его энергия, если расстояние между обкладками уменьшить в три раза.

Решение

Заряд конденсатора равен:

Изменение заряда будет равно:

Изменение энергии:

Ответ: 5 мкДж.

Источник питания на примере гидравлики

Давайте рассмотрим водобашню, в которой есть автоматическая подача воды. То есть сколько бы мы не потребляли воды из башни, ее уровень воды будет неизменным.

Схематически это будет выглядеть вот так:

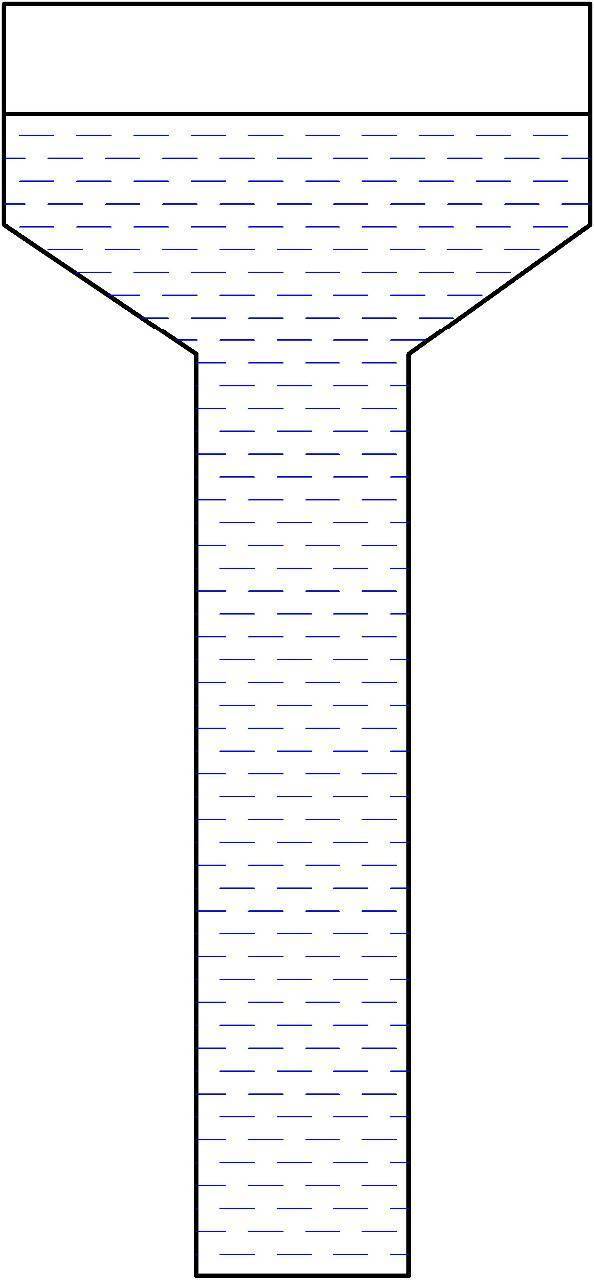
Башню с автоматической подачей воды можно считать источником питания. В химических же источниках питания происходит разряд, что ведет к тому, что уровень напряжения понижается при длительной работе. А что такое напряжение по аналогии с гидравликой? Это тот же самый уровень воды)

Давайте отпилим у водобашни верхнюю часть для наглядности. У нас получится цилиндр, который заполнен водой. Возьмем за точку отсчета уровень земли. Пусть он у нас будет равняться нулю.

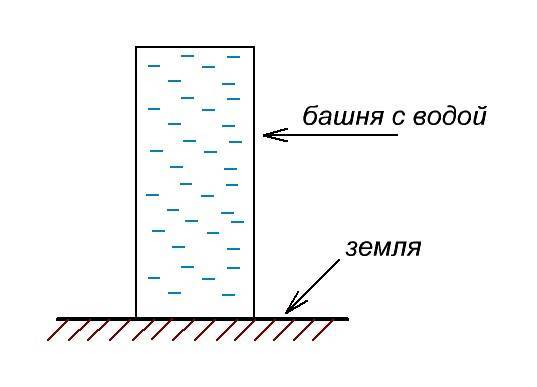
Теперь вопрос на засыпку. В каком случае давление на дно будет больше? Когда в башне немного воды

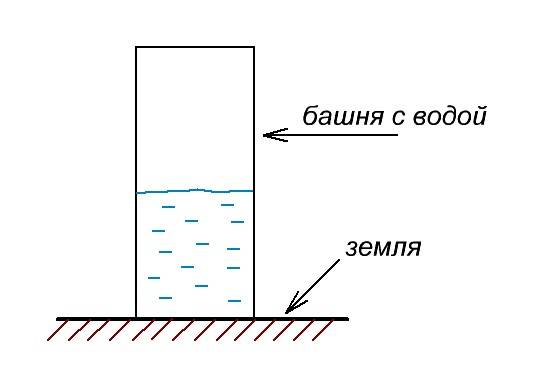
либо когда башня полностью залита водой так, что даже вода выходит за ее края

Разумеется, когда башня наполнена только наполовину водой, на дне башни давление меньше, чем тогда, когда в башне воды под завязку.

Думаю, не надо объяснять, что если в башне вообще нет воды, то никакого давления на дне башни не будет.

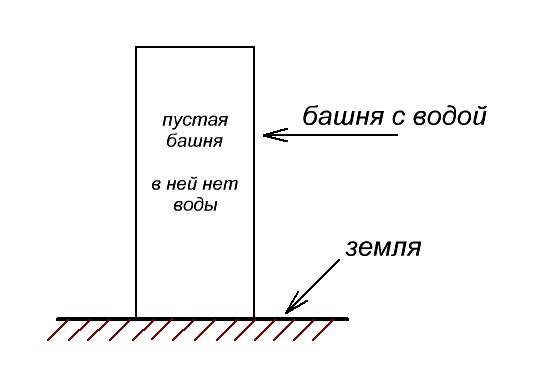
По тому же самому принципу работает батарейка или аккумулятор

На электрических схемах ее обозначение выглядит примерно вот так:

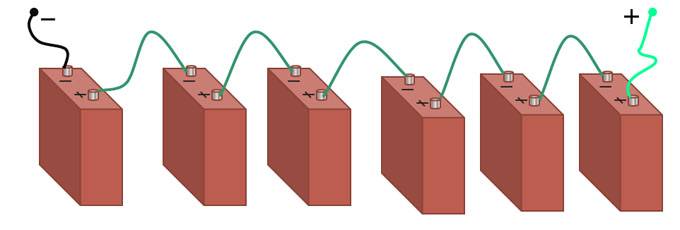
Также, чтобы получить необходимое напряжение, одноэлементные источники питания соединяют последовательно. На схеме это выглядит вот так:

Любой аккумулятор или источник постоянного тока имеет два полюса: «плюс» и «минус». Минус — это уровень земли, как в нашем примере с водобашней, а плюс — это напряжение, по аналогии с гидравликой это и будет тот самый уровень воды.

Электрические цепи. Последовательное и параллельное соединения проводников

Подробности

Просмотров: 420

«Физика – 10 класс»

Как выглядит зависимость силы тока в проводнике от напряжения на нём? Как выглядит зависимость силы тока в проводнике от его сопротивления?

От источника тока энергия может быть передана по проводам к устройствам, потребляющим энергию: электрической лампе, радиоприёмнику и др. Для этого составляют электрические цепи различной сложности.

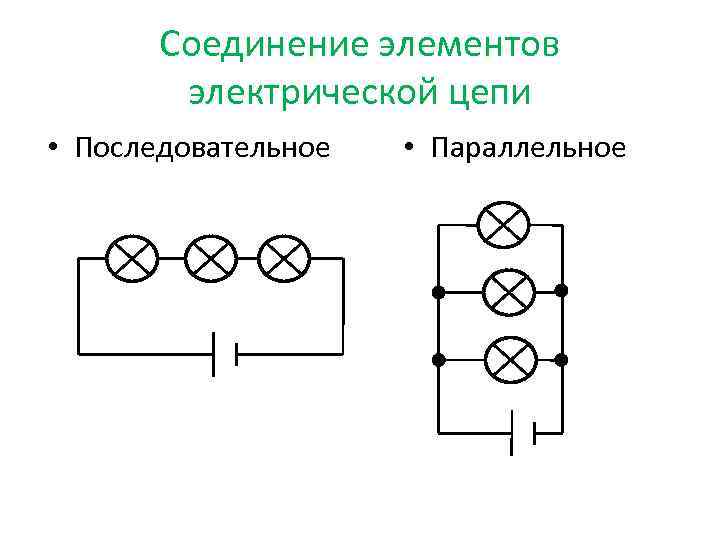
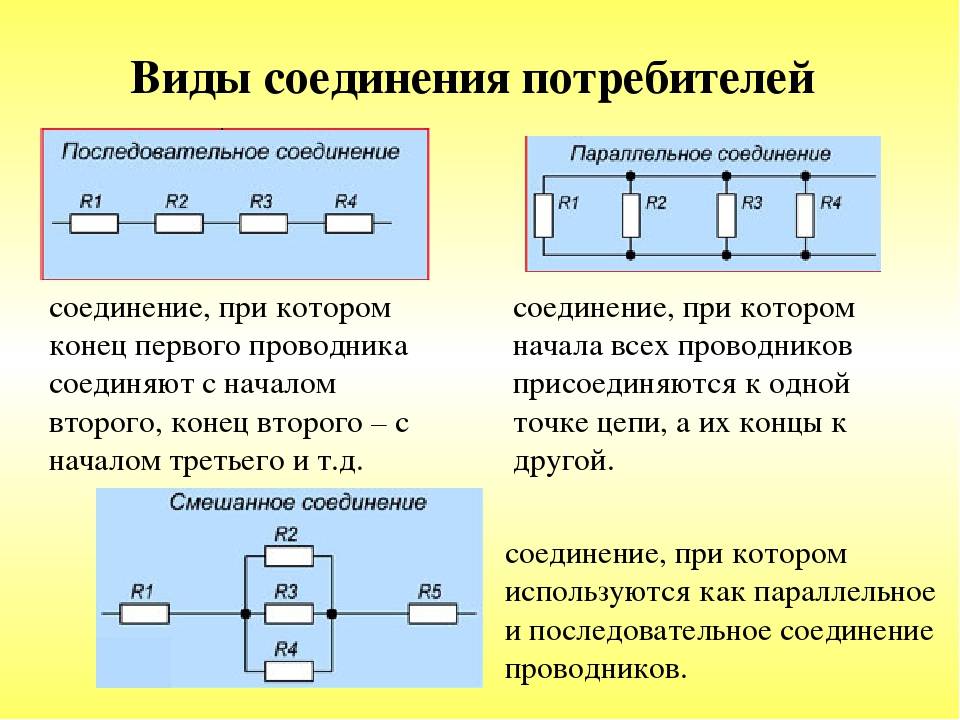
К наиболее простым и часто встречающимся соединениям проводников относятся последовательное и параллельное соединения.

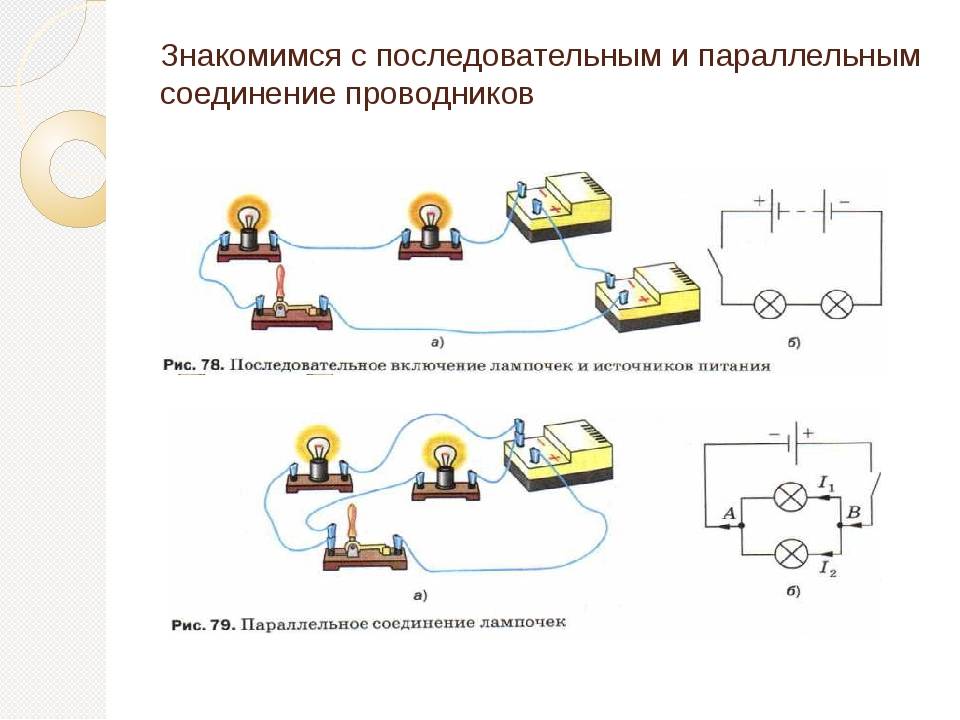
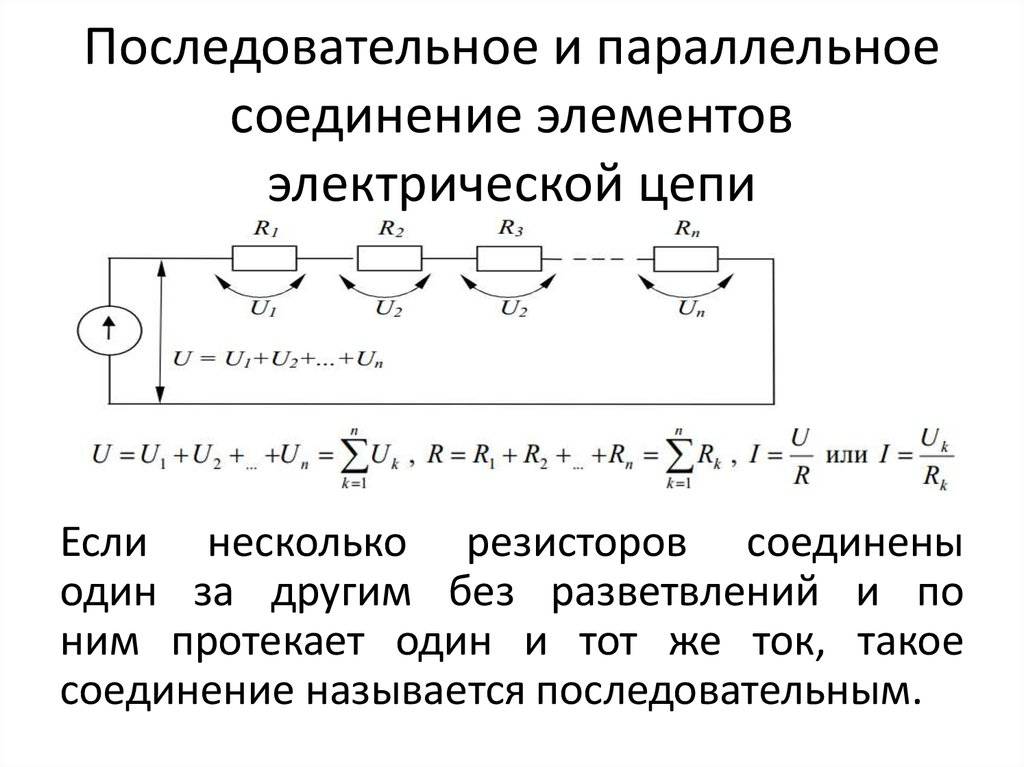
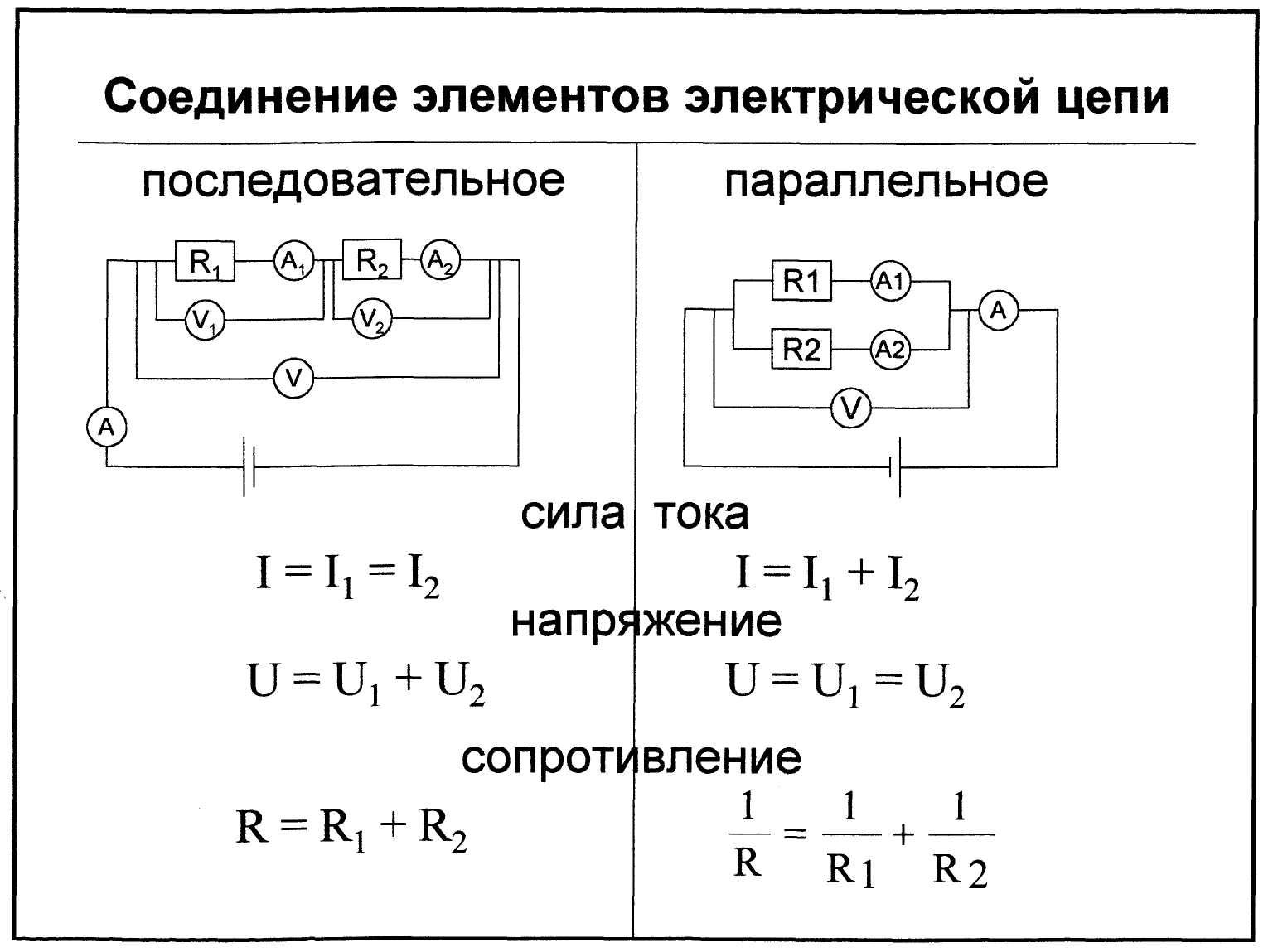
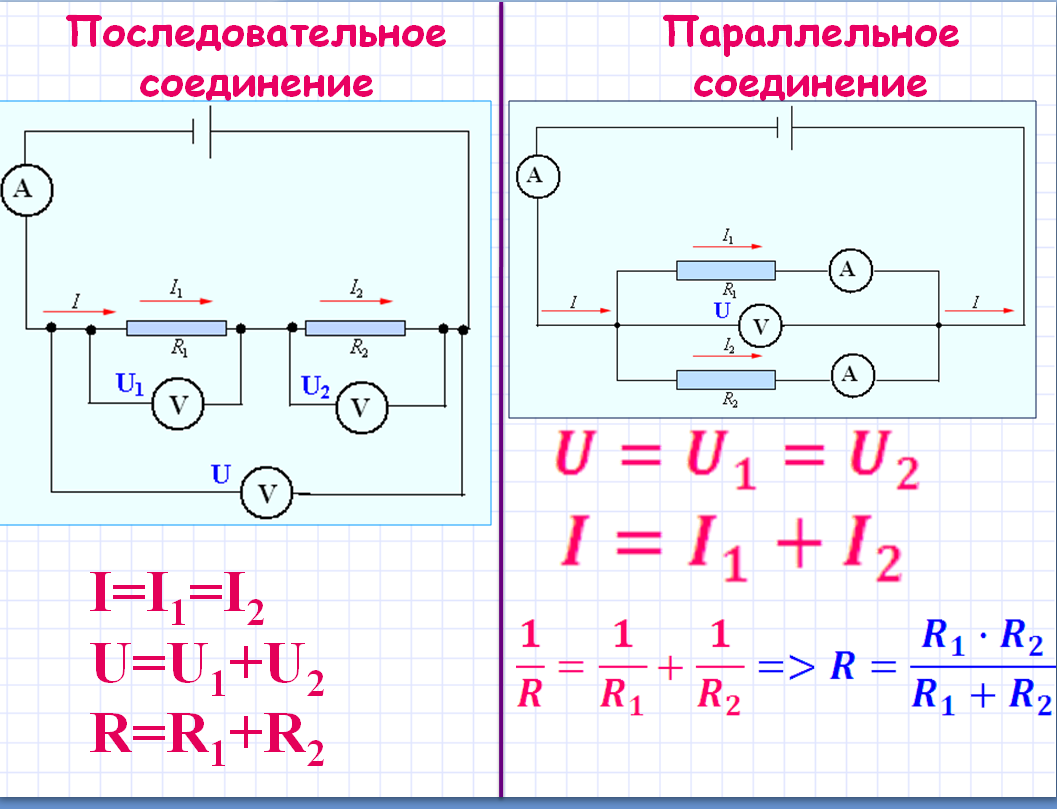
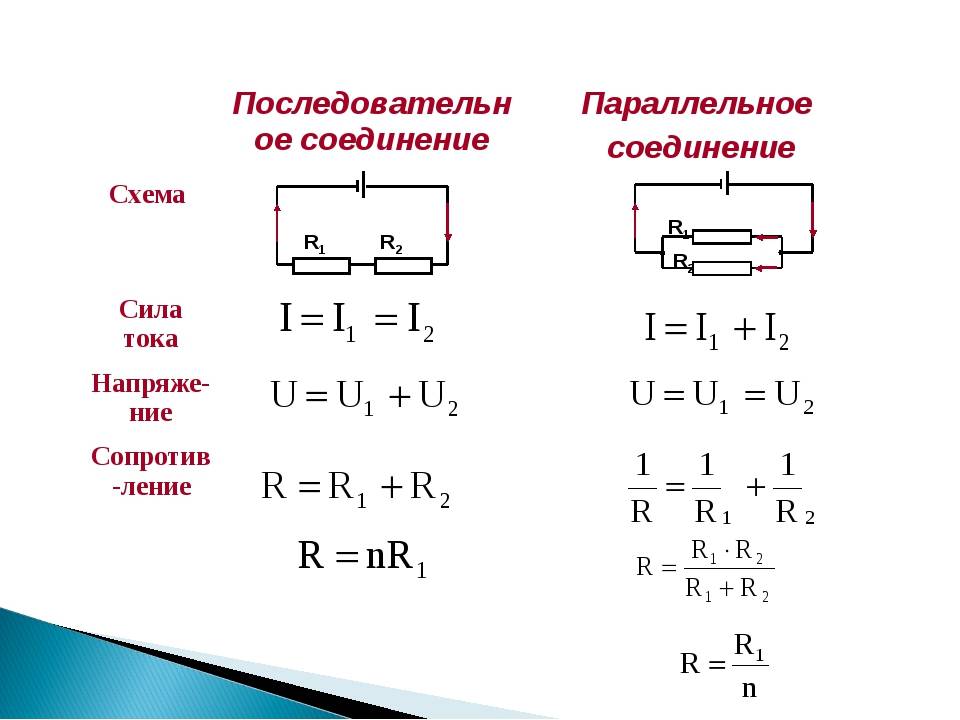
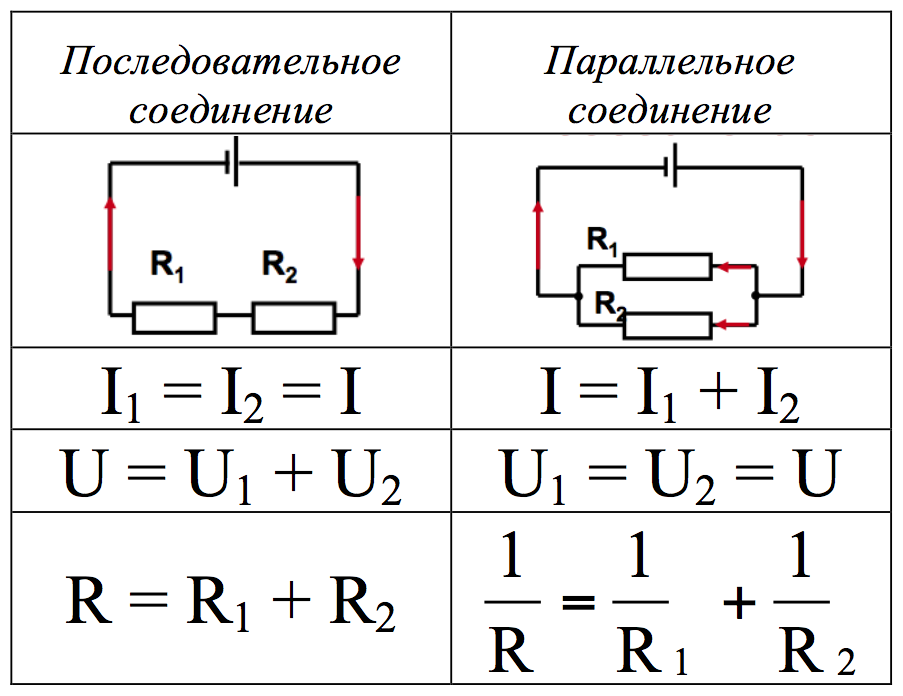
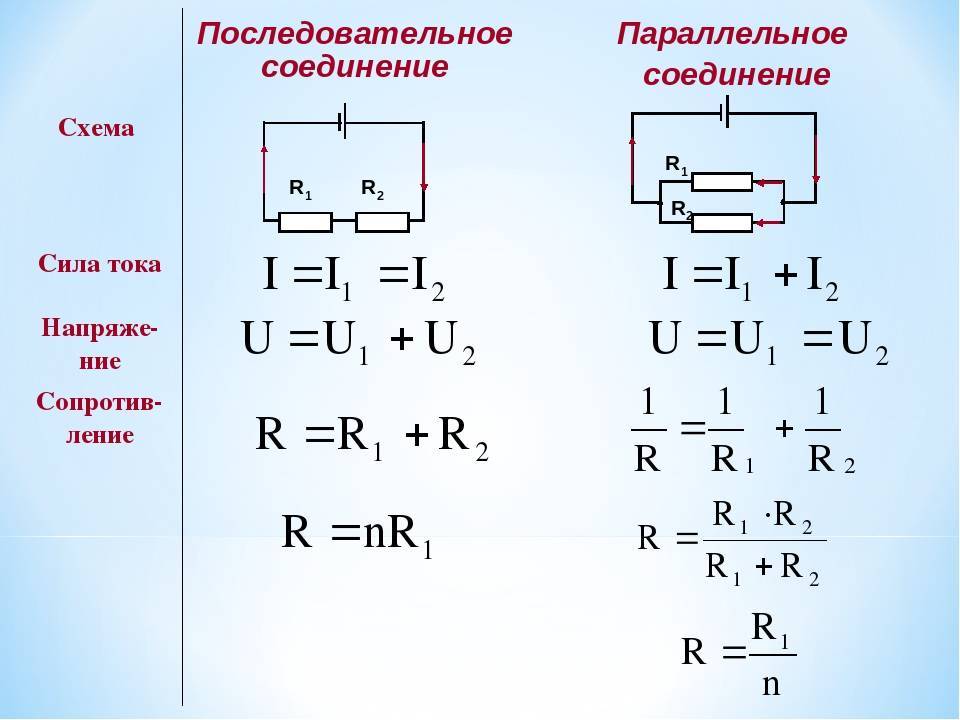
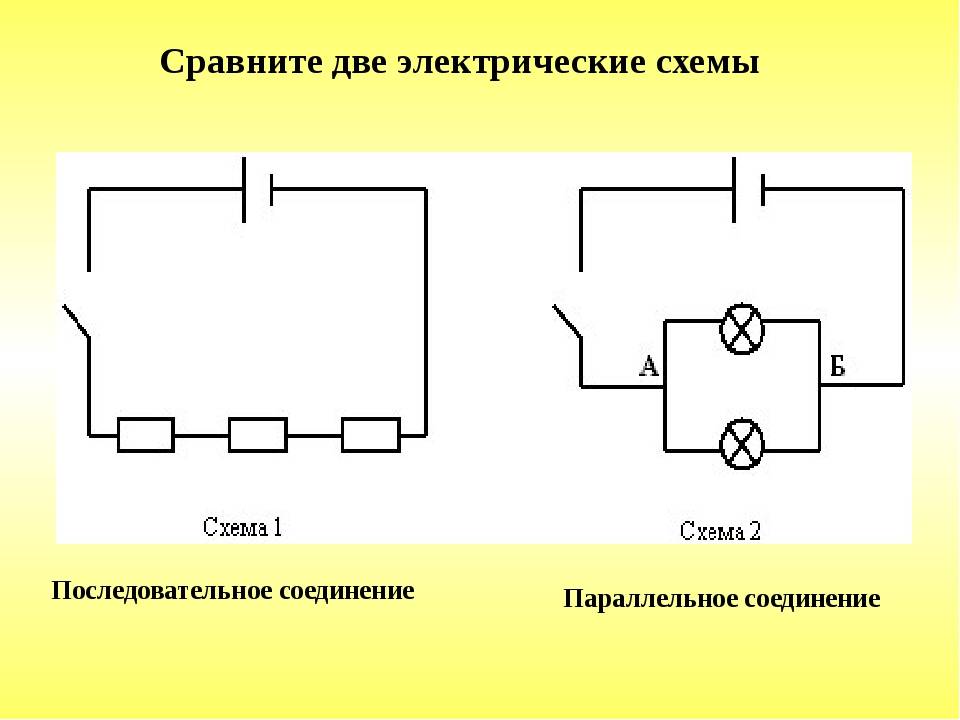
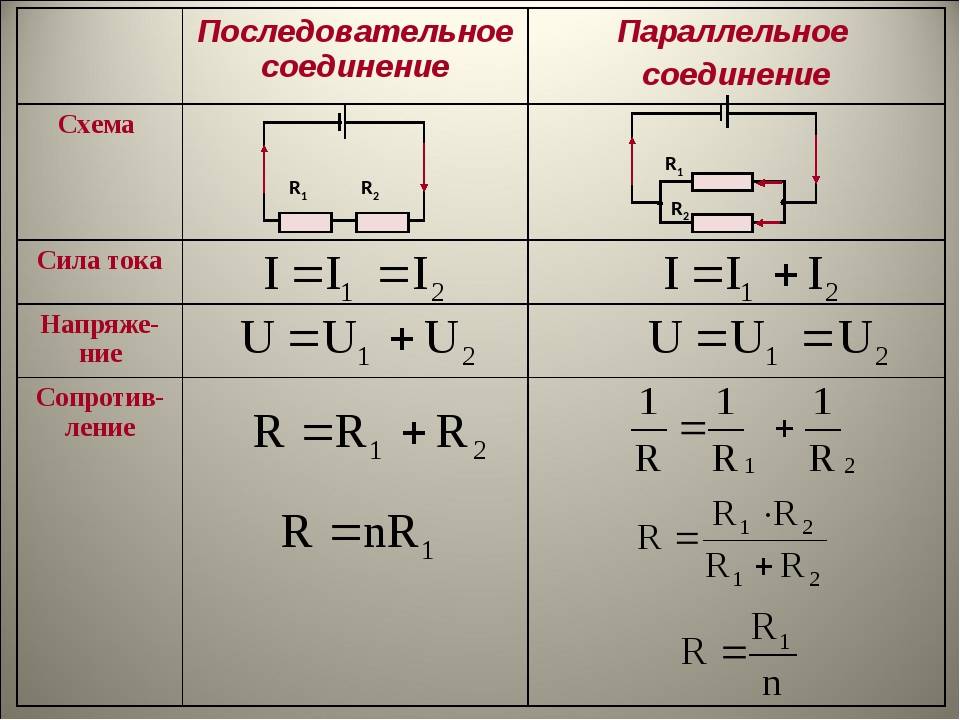
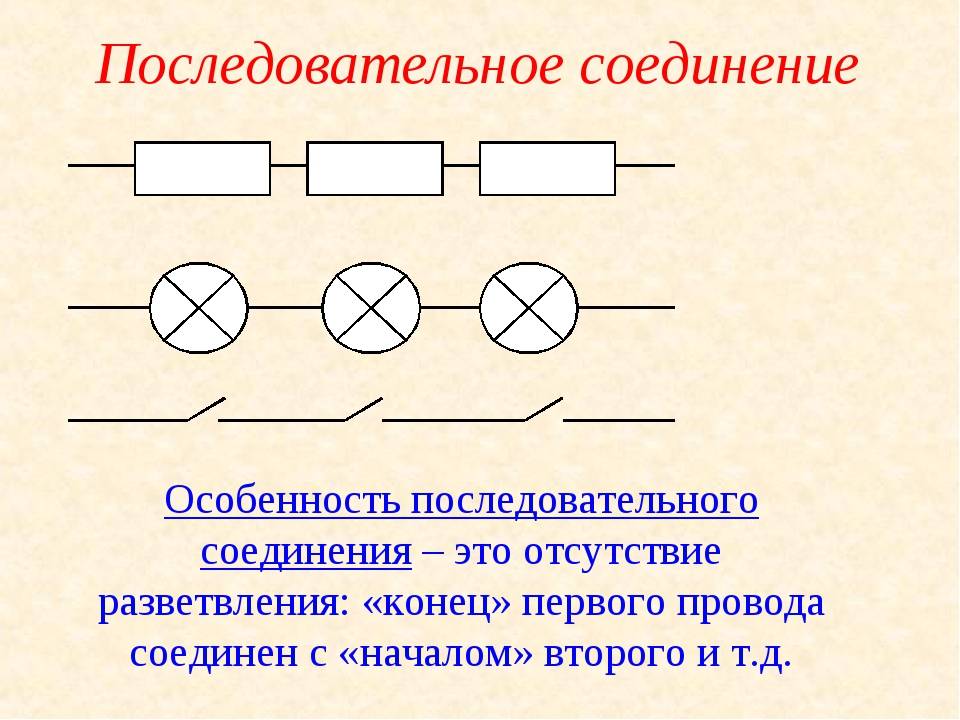
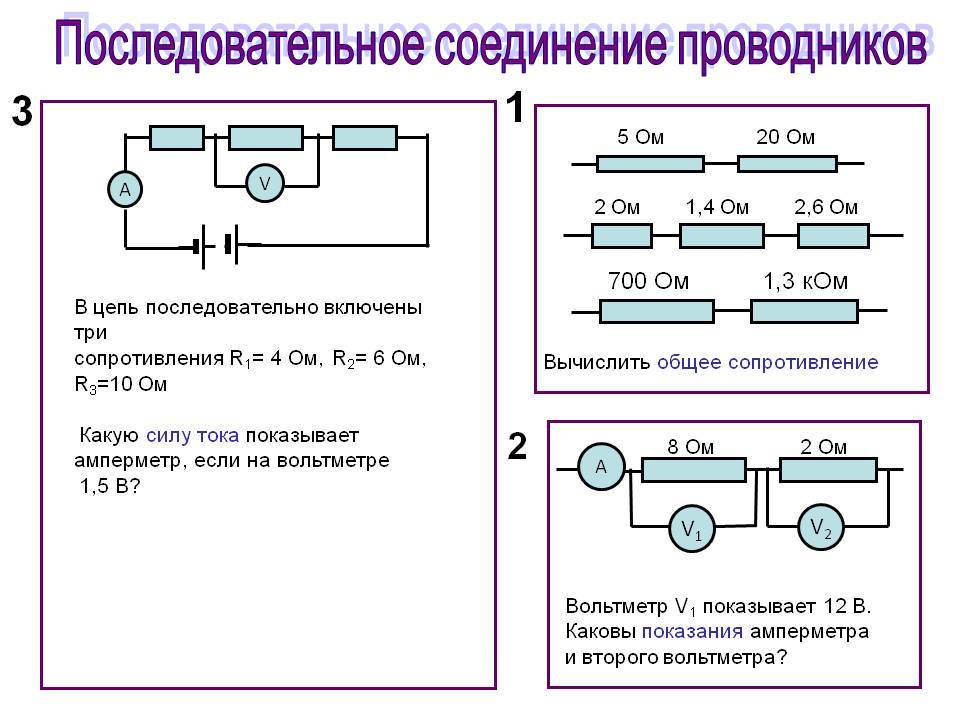
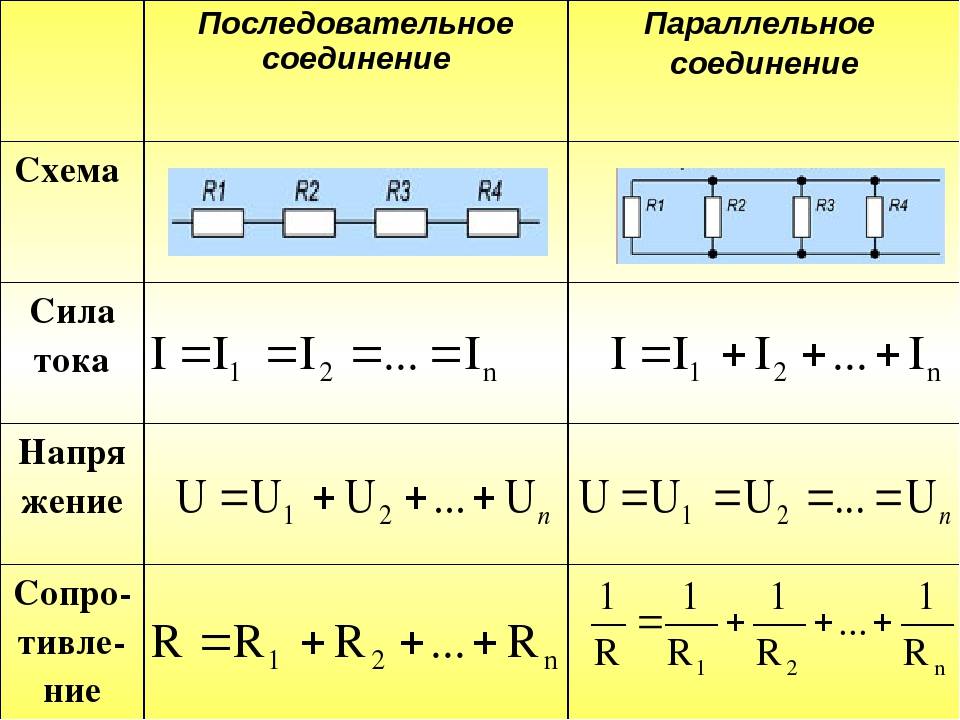
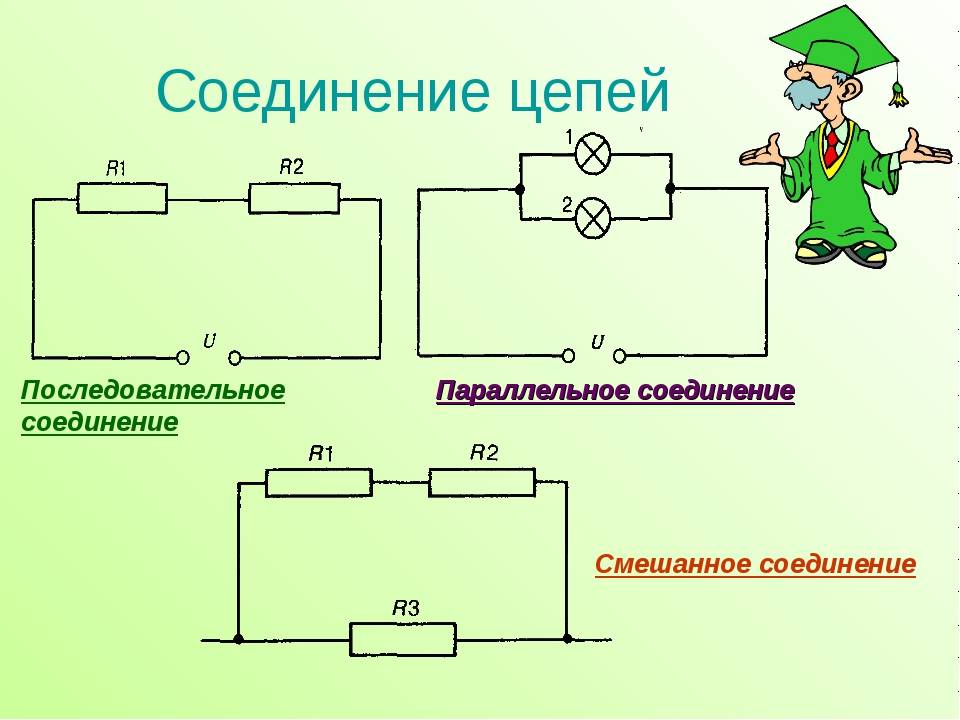
Последовательное соединение проводников.

При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочерёдно друг за другом. На рисунке (15.5, а) показано последовательное соединение двух проводников 1 и 2, имеющих сопротивления R₁ и R₂. Это могут быть две лампы, две обмотки электродвигателя и др.

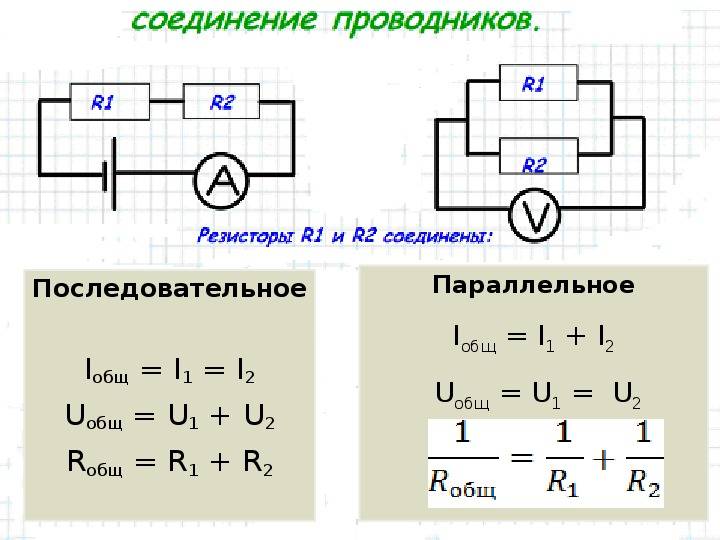
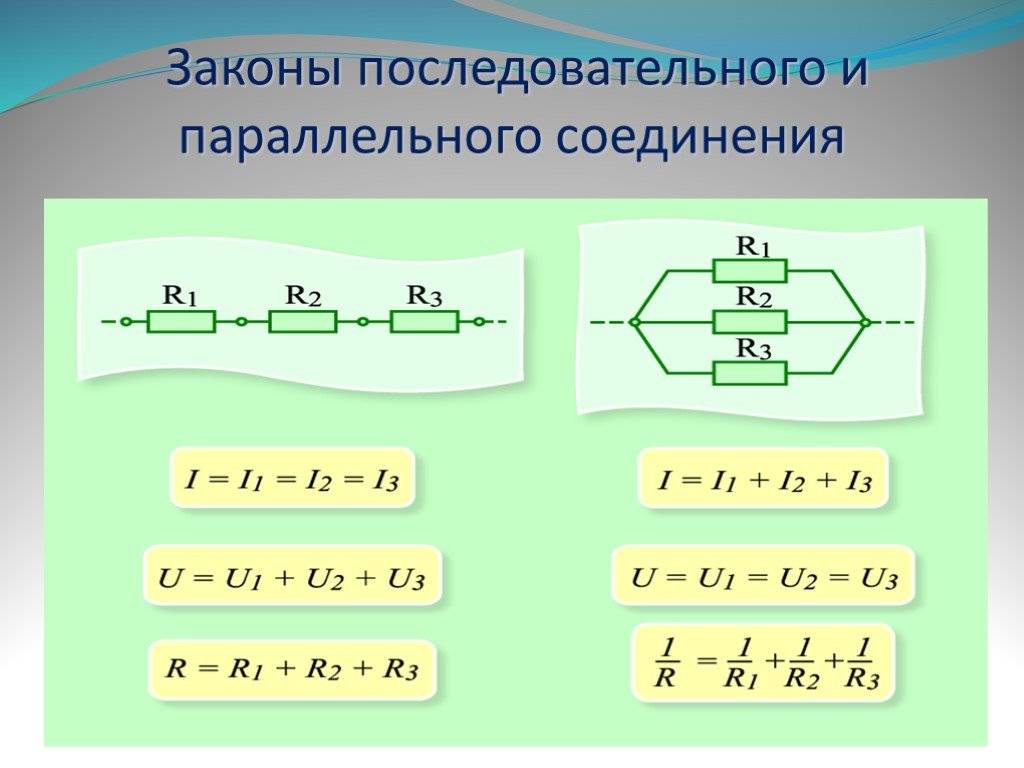
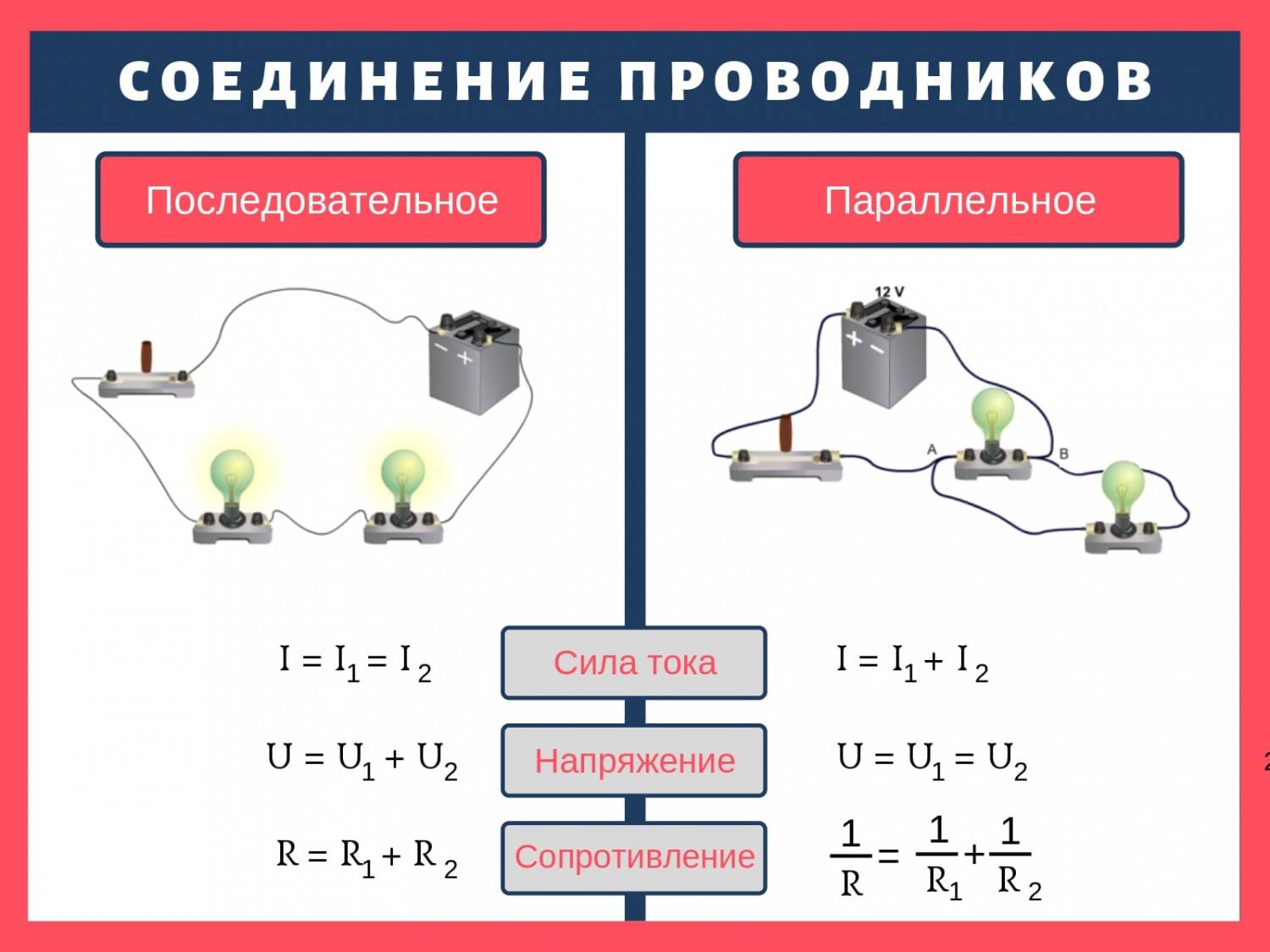
Сила тока в обоих проводниках одинакова, т. е.

I₁ = I₂ = I.         (15.5)

В проводниках электрический заряд в случае постоянного тока не накапливается, и через любое поперечное сечение проводника за определённое время проходит один и тот же заряд.

Напряжение на концах рассматриваемого участка цепи складывается из напряжений на первом и втором проводниках:

U = U₁ + U₂.

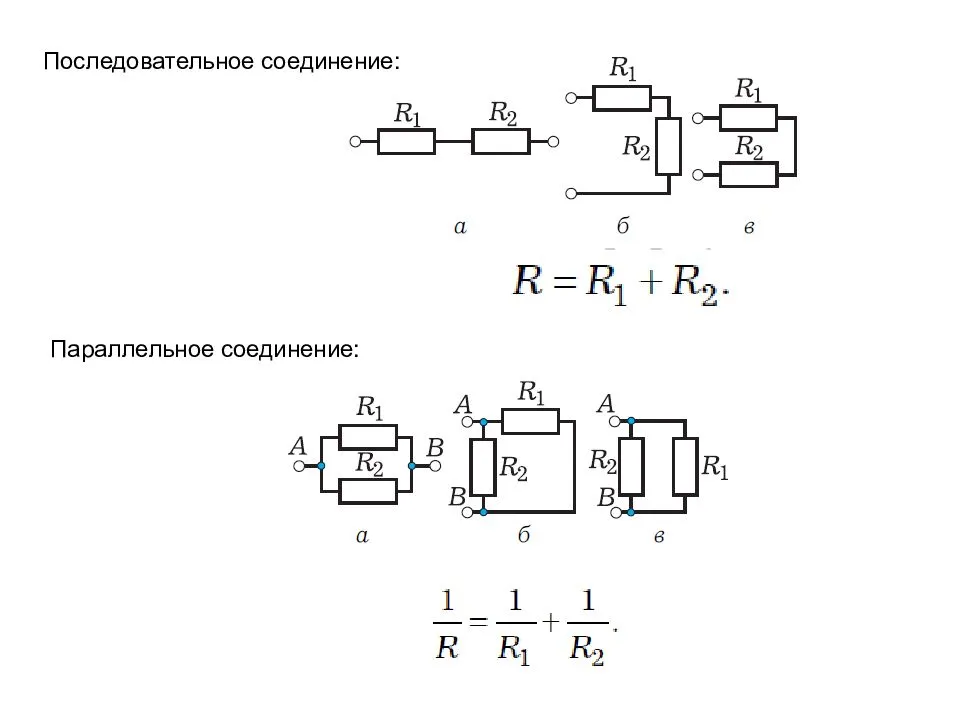
Применяя закон Ома для всего участка в целом и для участков с сопротивлениями проводников R1 и R2, можно доказать, что полное сопротивление всего участка цепи при последовательном соединении равно:

R = R₁ + R₂.         (15.6)

Это правило можно применить для любого числа последовательно соединённых проводников.

Напряжения на проводниках и их сопротивления при последовательном соединении связаны соотношением

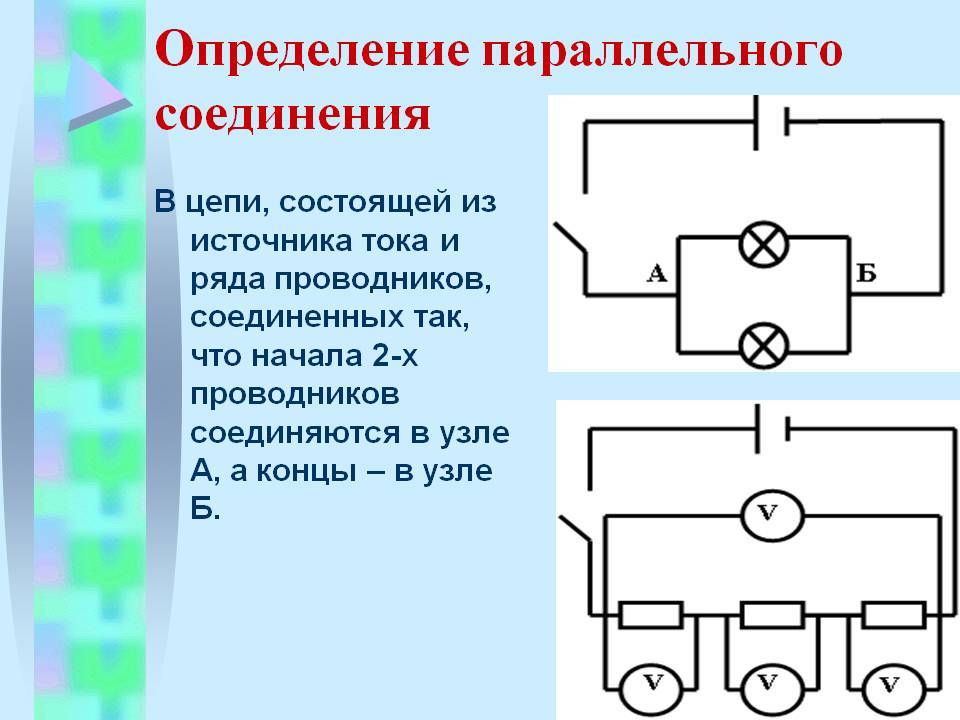
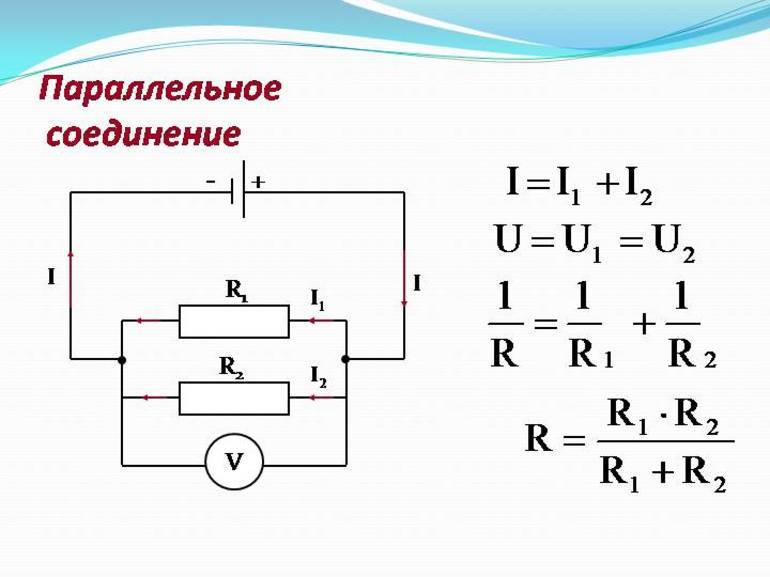
Параллельное соединение проводников.

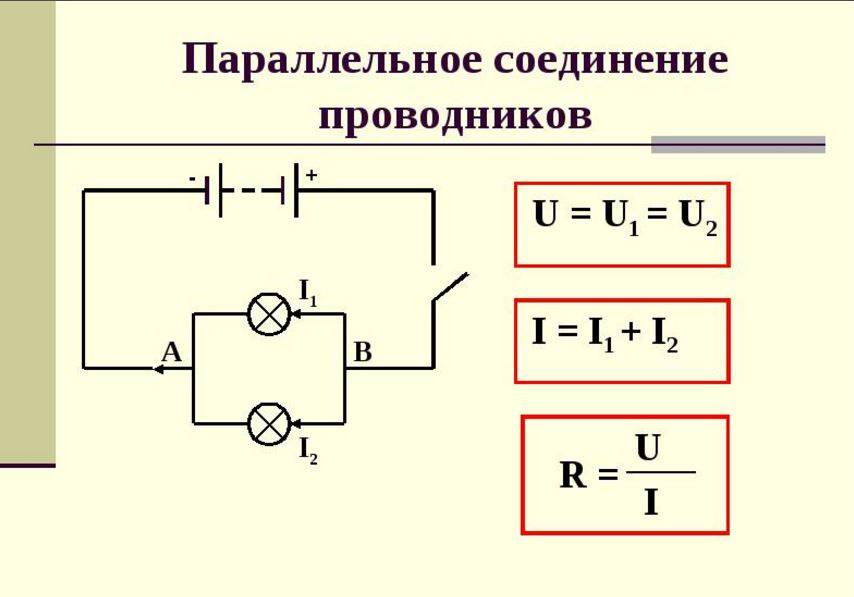
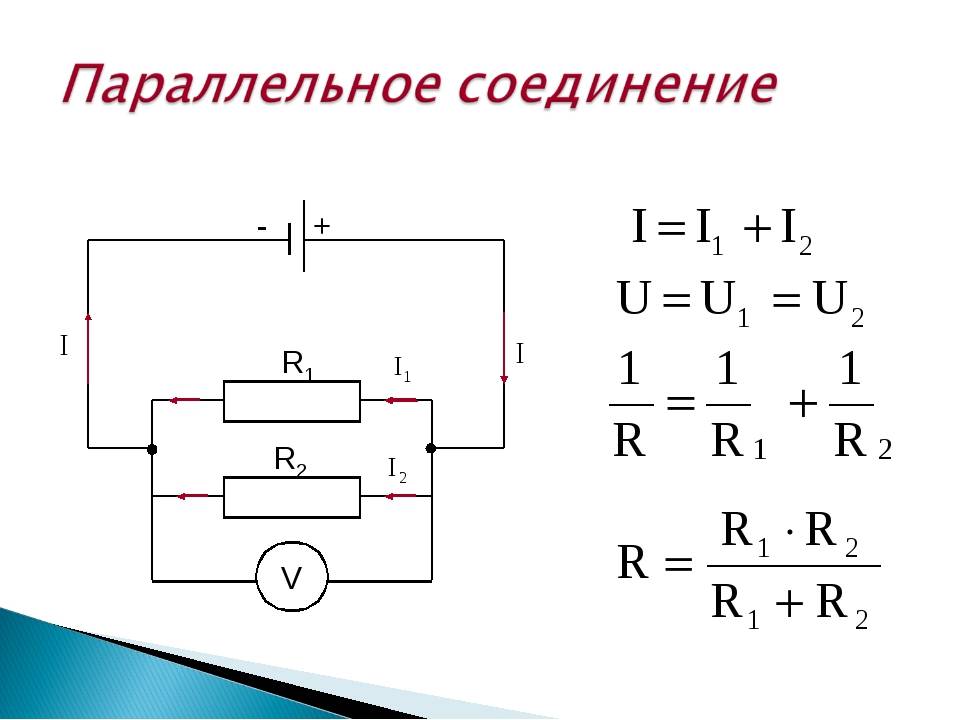
На рисунке (15.5, б) показано параллельное соединение двух проводников 1 и 2 сопротивлениями R₁ и R₂. В этом случае электрический ток I разветвляется на две части. Силу тока в первом и втором проводниках обозначим через I₁ и I₂.

Так как в точке а — разветвлении проводников (такую точку называют узлом) — электрический заряд не накапливается, то заряд, поступающий в единицу времени в узел, равен заряду, уходящему из узла за это же время. Следовательно,

I = I₁ + I₂.         (15.8)

Напряжение U на концах проводников, соединённых параллельно, одинаково, так как они присоединены к одним и тем же точкам цепи.

В осветительной сети обычно поддерживается напряжение 220 В. На это напряжение рассчитаны приборы, потребляющие электрическую энергию. Поэтому параллельное соединение — самый распространённый способ соединения различных потребителей. В этом случае выход из строя одного прибора не отражается на работе остальных, тогда как при последовательном соединении выход из строя одного прибора размыкает цепь. Применяя закон Ома для всего участка в целом и для участков проводников сопротивлениями R₁ и R₂, можно доказать, что величина, обратная полному сопротивлению участка ab, равна сумме величин, обратных сопротивлениям отдельных проводников:

Отсюда следует, что для двух проводников

Напряжения на параллельно соединённых проводниках равны: I₁R₁ = I₂R₂. Следовательно,

Обратим внимание на то, что если в какой-то из участков цепи, по которой идёт постоянный ток, параллельно к одному из резисторов подключить конденсатор, то ток через конденсатор не будет идти, цепь на участке с конденсатором будет разомкнута. Однако между обкладками конденсатора будет напряжение, равное напряжению на резисторе, и на обкладках накопится заряд q = CU. Рассмотрим цепочку сопротивлений R — 2R, называемую матрицей (рис

15.6)

Рассмотрим цепочку сопротивлений R — 2R, называемую матрицей (рис. 15.6).

На последнем (правом) звене матрицы напряжение делится пополам из-за равенства сопротивлений, на предыдущем звене напряжение тоже делится пополам, поскольку оно распределяется между резистором сопротивлением R и двумя параллельными резисторами сопротивлениями 2R и т. д. Эта идея — деления напряжения — лежит в основе преобразования двоичного кода в постоянное напряжение, что необходимо для работы компьютеров.

Следующая страница «Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников»»

Назад в раздел «Физика – 10 класс, учебник Мякишев, Буховцев, Сотский»

Законы постоянного тока – Физика, учебник для 10 класса – Класс!ная физика

Электрический ток. Сила тока — Закон Ома для участка цепи. Сопротивление — Электрические цепи. Последовательное и параллельное соединения проводников — Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» — Работа и мощность постоянного тока — Электродвижущая сила — Закон Ома для полной цепи — Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»

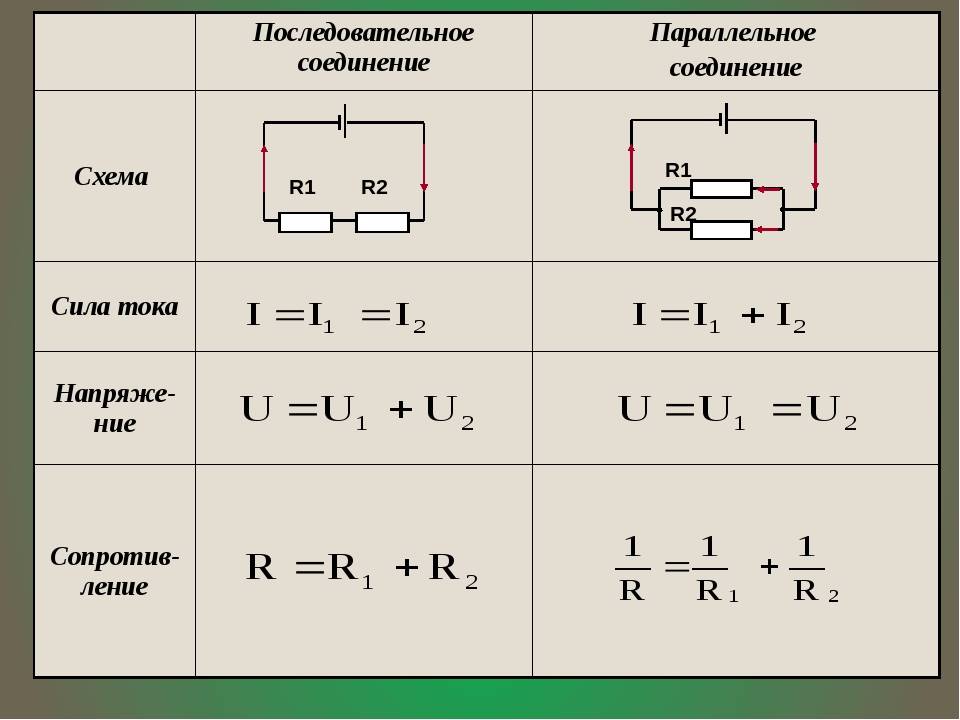
Разница между последовательным и параллельным соединением, преимущества и недостатки

Принципиальные отличия между последовательным и параллельным соединение проводников по ключевым электротехническим параметрам приведены в таблице:

Параметр/тип соединения	Последовательное	Параллельное
Электросопротивление	Равняется сумме электросопротивлений всех электропотребителей.	Меньше значения электросопротивления каждого отдельного из подключенных электроприборов.
Напряжение	Равняется совокупному вольтажу всех электропотребителей.	Одинаковая величина на всех участках электроцепи.
Сила тока	Одинаковая величина на всех участках электроцепи.	Равняется совокупному значению токов на каждом из приборов.

За счет своих особенностей каждый из типов сборки цепей имеет свои преимущества и недостатки. Это позволяет использовать данные способы для решения разных электротехнических задач.

Плюсы и минусы последовательного соединения

Основными преимуществам электроцепей из последовательно соединенных приборов являются их следующие особенности:

• простота проектирования и построения схемы;
• низкая стоимость комплектации;
• возможность подключения приборов, рассчитанных на меньшее рабочее напряжение, по сравнению с номинальным напряжением сети;
• выполнение функции регулирования тока – обеспечивает равномерные нагрузки на все приборы.

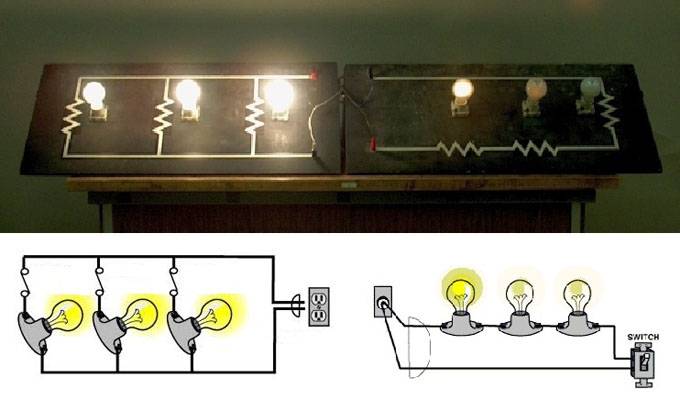
Однако у этого способа компоновки электросхемы есть и серьезные недостатки. Главным из них является ненадежность цепи из последовательно соединенных проводников. При выходе из строя любого из подключенных приборов, происходит отключение всей цепи.

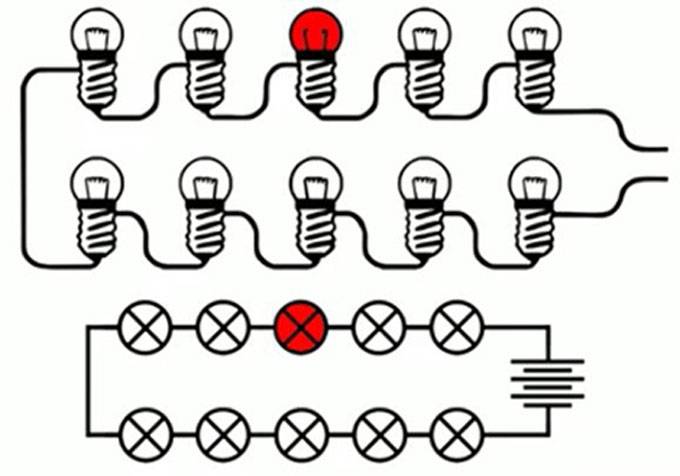
Кроме того, минусом является снижение напряжения при увеличении количества подключенных потребителей. Примером может служить последовательное соединение нескольких ламп. Чем больше осветительных приборов подключено таким способом к источнику электропитания, тем менее яркий свет они будут давать.

Плюсы и минусы параллельного соединения

При использовании параллельного соединения проводников обеспечиваются такой набор преимуществ:

• стабильность напряжения на электроприборах, вне зависимости от их числа;
• возможность включения или отключения отдельных участков в нужный момент без нарушения работы всей электроцепи;
• надежность – при выходе одного или нескольких компонентов из строя сама электроцепь продолжает сохранять работоспособность.

Недостатком является более сложный расчет и сложная схема, использование которой повышает стоимость комплектации электросети.

Не допускается подключение приборов, с номинальным рабочим вольтажом меньше сетевого. Параллельное соединение аккумуляторов с разным значением вольтажа связано с перетеканием тока в АКБ с меньшей его величиной, что может вызывать ускоренный износ батареи.

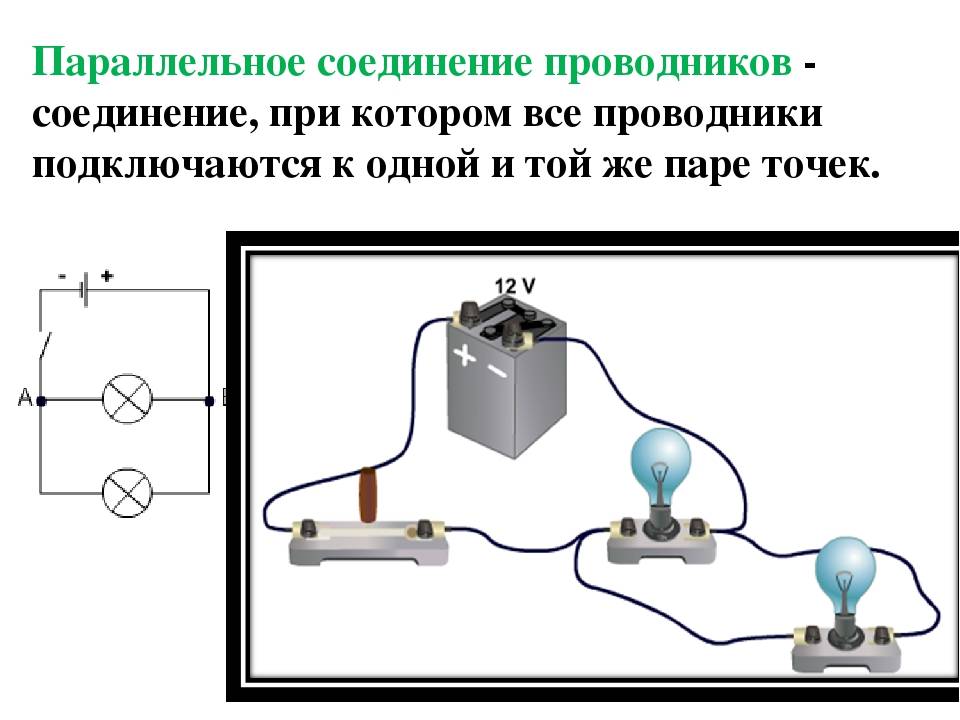
Параллельное соединение проводников

В параллельной схеме проводники представляют собой набор резисторов, одни концы которых собираются в один узел, а другие – во второй узел. Предполагается, что напряжение в параллельном типе соединения одинаковое на всех участках цепи. Параллельные участки электроцепи носят название ветвей и проходят между двумя соединительными узлами, на них имеется одинаковое напряжение. Такое напряжение равно значению на каждом проводнике. Сумма показателей, обратных сопротивлениям ветвей, является обратной и по отношению к сопротивлению отдельного участка цепи параллельной схемы.

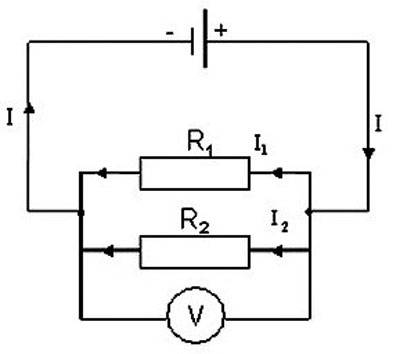
При параллельном и последовательном соединениях отличается система расчета сопротивлений отдельных проводников. В случае параллельной схемы ток уходит по ветвям, что способствует повышению проводимости цепи и уменьшает совокупное сопротивление. При параллельном подключении нескольких резисторов с аналогичными значениями совокупное сопротивление такой электроцепи будет меньше одного резистора число раз, равное числу резисторов в схеме.

В каждой ветви предусмотрено по одному резистору, и электроток при достижении точки разветвления делится и расходится к каждому резистору, его итоговое значение равно сумме токов на всех сопротивлениях. Все резисторы заменяются одним эквивалентным резистором. Применяя закон Ома, становится понятным значение сопротивления – при параллельной схеме суммируются значения, обратные сопротивлениям на резисторах.

При данной схеме значение тока обратно пропорционально значению сопротивления. Токи в резисторах не взаимосвязаны, поэтому при отключении одного из них это никоим образом не отразится на остальных. По этой причине такая схема используется во множестве устройств.

Рассматривая возможности применения параллельной схемы в быту, целесообразно отметить систему освещения квартиры. Все лампы и люстры должны быть соединены параллельно, в таком случае включение и отключение одного из них никак не влияет на работу остальных ламп. Таким образом, добавляя выключатель каждой лампочки в ветвь цепи, можно включать и отключать соответствующий светильник по необходимости. Все остальные лампы работают независимо.

Все электроприборы объединяются параллельно в электросеть с напряжением 220 В, затем они подключаются к распределительному щитку. То есть все приборы подключаются независимо от подключения прочих устройств.