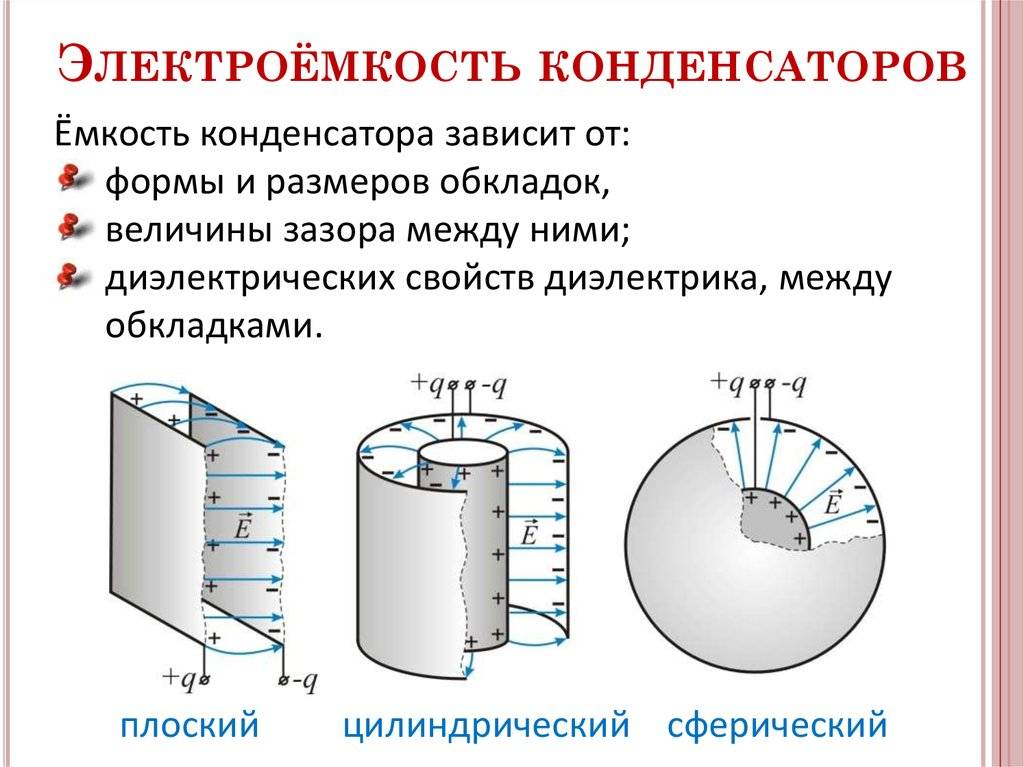
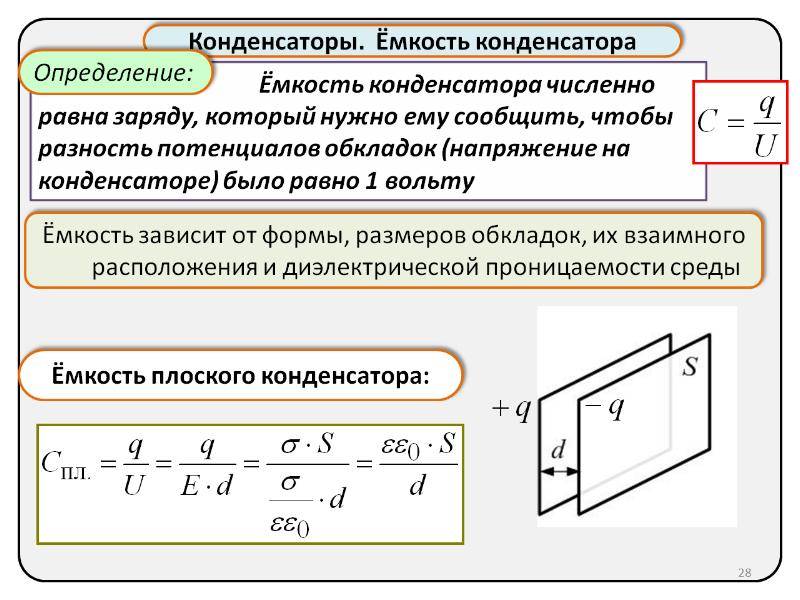
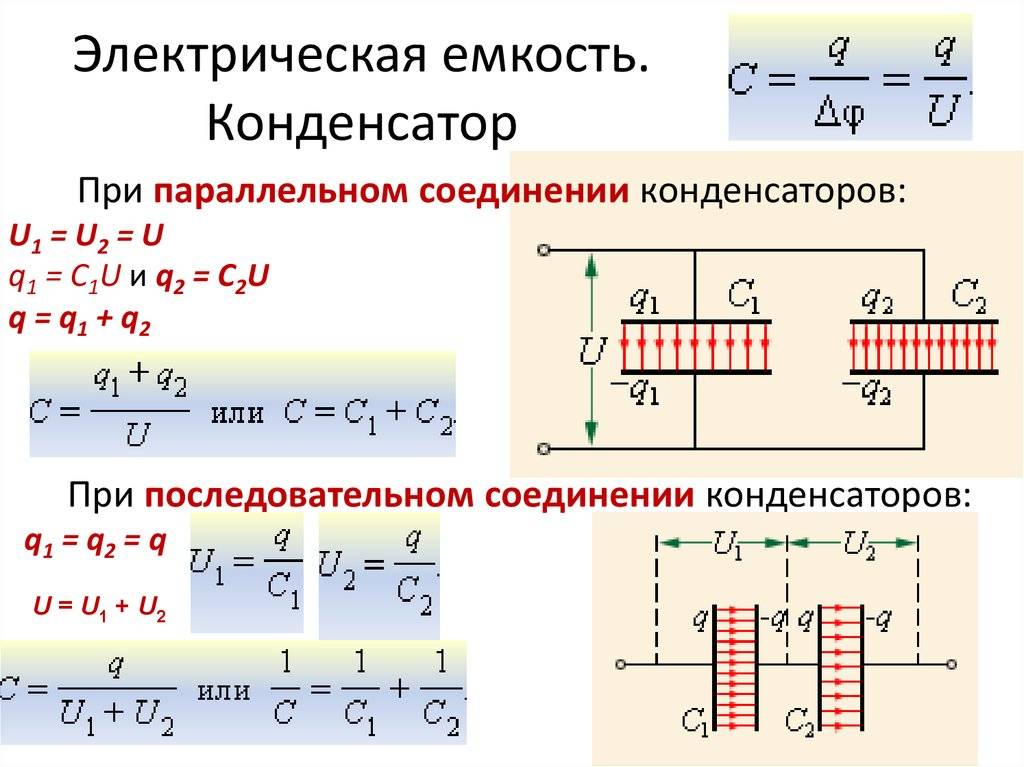
Что такое конденсатор, где применяется и для чего нужен

Что такое конденсатор

Изделия этой категории созданы на основе известного физического процесса накопления электрического заряда на параллельно расположенных пластинах с диэлектрическим промежутком, подключенных к источнику тока. Максимальное количество энергии определяет емкость, которая по стандартам системы СИ выражается в фарадах (Ф). С учетом чрезмерной величины базовой единицы измерения для удобства применяют уменьшенные (дольные) значения:

• миллифарады, мф, mF – 10-3Ф;
• нанофарады, нф, mF – 10-9Ф;
• пикофарады, пкф, pF – 10-12Ф и др.

К сведению. С учетом типичных сокращений несложно догадаться, что мкф – это микрофарады (10-9Ф). Маркировка 12 мкф = 12*10-9 = 0,000000012 Ф.

Устройство и характеристики конденсатора

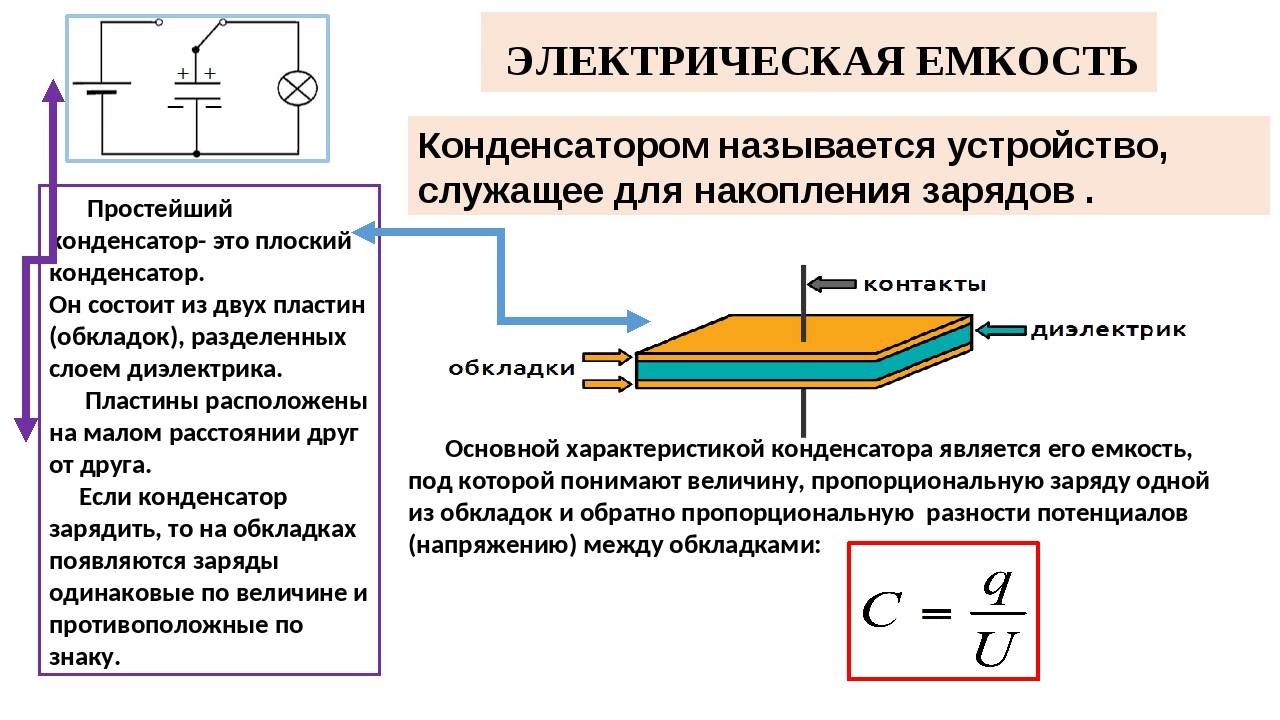
Конструкция конденсатора представляет собой две токопроводящие пластины, разделённые диэлектриком. Если приложить к пластинам напряжение от источника постоянного тока, то ток короткое время будет протекать через конденсатор, и он зарядится. На его пластинах (обкладках) накопится напряжение, равное напряжению источника. Длительность протекания тока и ёмкость его заряда зависят от площади обкладок и расстояния между ними. Ёмкость обозначается буквой С и измеряется в фарадах. Единица измерения в системе СИ – 1Ф (F). Обозначение принято в честь физика из Англии М. Фарадея.

Внимание! Ёмкость 1Ф – очень большая величина. Если рассматривать Землю как уединённый проводник в форме шара, то ёмкость составила бы около 700 мкФ

Поэтому электротехнические элементы измеряют в малых величинах: пикофарадах (пФ), нанофарадах (нФ), микрофарадах (мкФ).

Единицы измерения ёмкости

В цепях постоянного и переменного тока ёмкостной элемент ведёт себя по-разному. Если постоянный ток конденсатор через себя не пропускает, то переменному току, проходящему через него, оказывает определённое сопротивление. Это ещё одна важная характеристика конденсатора – ёмкостное сопротивление RC.

Сопротивление из разряда реактивных сопротивлений, рассчитывается по формуле:

Rс =1/6,28*f*C,

где:

• Rc – емкостное сопротивление, Ом;
• 6,28 – 2 π;
• f – частота тока, Гц;
• C – емкость данного конденсатора, Ф.

Важно! Как видно из формулы, для токов разной частоты сопротивление одного и того же элемента меняется. Чем выше частота тока, тем ниже ёмкостное сопротивление конденсатора

Различают конденсаторы постоянной и переменной ёмкости. Вторые имеют конструкцию, в результате которой изменяется расстояние между пластинами.

По типу исполнения конденсаторы постоянной ёмкости бывают:

• полярные электролитические;
• однослойные и многослойные керамические;
• высоковольтные керамические;
• полиэстеровые;
• танталовые;
• полипропиленовые конденсаторы.

Конструкция зависит от порядкового разряда ёмкости элемента, применяемого материала для пластин и диэлектрика.

Как заряжается и разряжается конденсатор?

При подключении к источнику постоянного тока, обкладки конденсатора заряжаются, одна приобретает положительный потенциал, а другая отрицательный. Между обкладками противоположные по знаку, но равные по значению, электрические заряды создают электрическое поле. Когда напряжения станут одинаковыми и на обкладках, и на источнике подаваемого тока, движение электронов прекратится и зарядка конденсатора закончится. Определенный промежуток времени конденсатор сохраняет заряды и выполняет функции автономного источника электроэнергии. В таком состоянии он может находиться достаточно долгое время. Если вместо источника, включить в цепь резистор, то конденсатор разрядится на него.

Математическая модель конденсатора. Обозначение.

Конденсатор имеет обычно два вывода. Работу конденсатора описывает следующее соотношение, которое и определяет его применение в схемотехнике. [Напряжение на конденсаторе в момент T] = [Напряжение на конденсаторе в начальный момент T0] + интеграл от [T0] до [T] ([Сила тока через выводы конденсатора] / [Емкость конденсатора]) по [Времени].

Более привычно эта формула выглядит так:

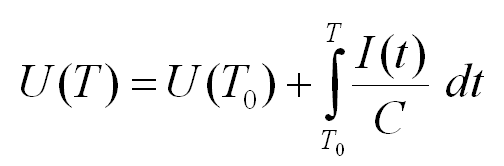
В случае, если через конденсатор идет постоянный ток, то формула приобретает вид: [Напряжение на конденсаторе в момент T] = [Напряжение на конденсаторе в начальный момент T0] + [Сила тока через выводы конденсатора] * ([T1] – [T0]) / [Емкость конденсатора]

Емкость конденсатора измеряется в Фарадах. Конденсатор емкостью 1 Ф за 1 с током в 1 А заряжается на 1 V. Обычно в схемах используются конденсаторы от 1 пикофарады до 100 миллифарад. Хотя сейчас бывают конденсаторы емкостью 10 Ф и выше.

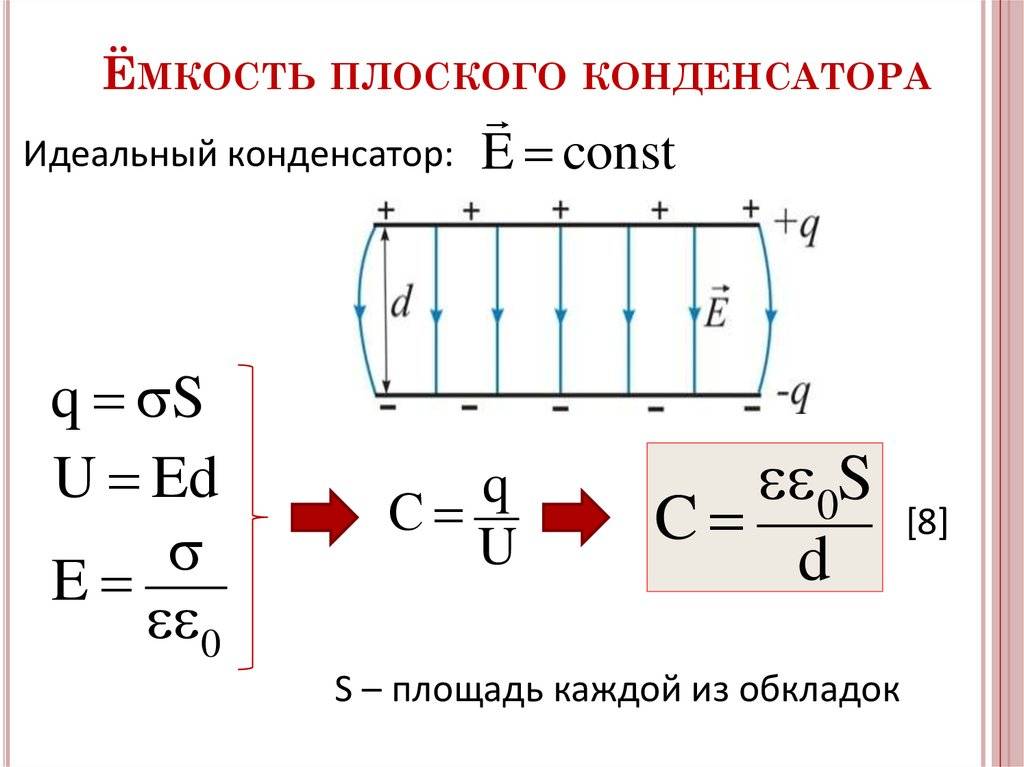
Физически конденсатор состоит из двух пластин, между которыми проложен диэлектрик. Один вывод конденсатора подключен к одной пластине, другой вывод – к другой пластине. На пластинах накапливается заряд.

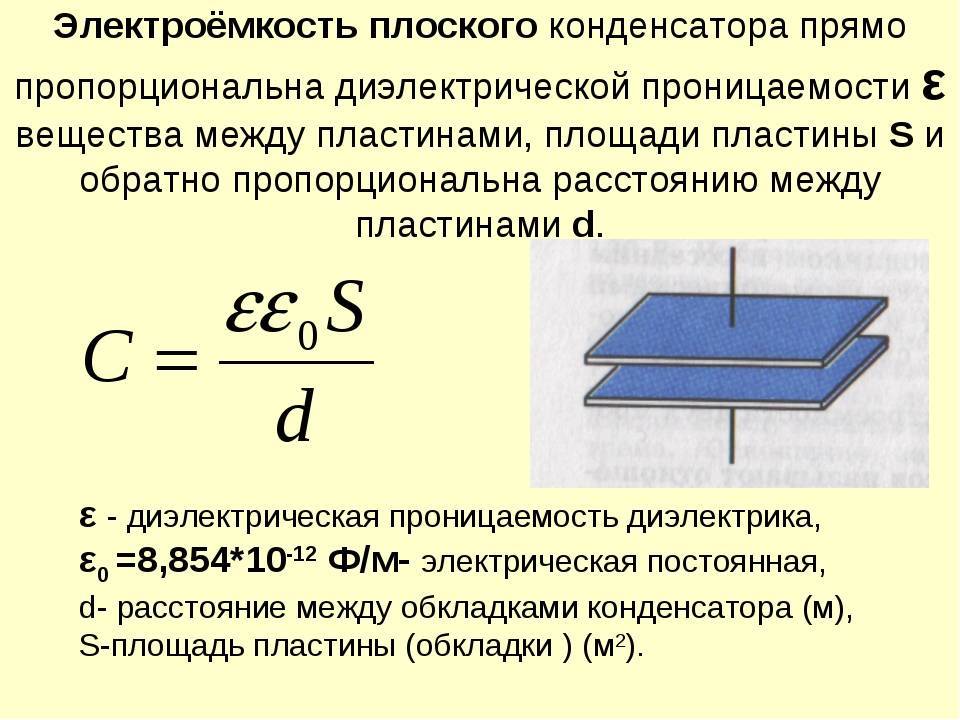
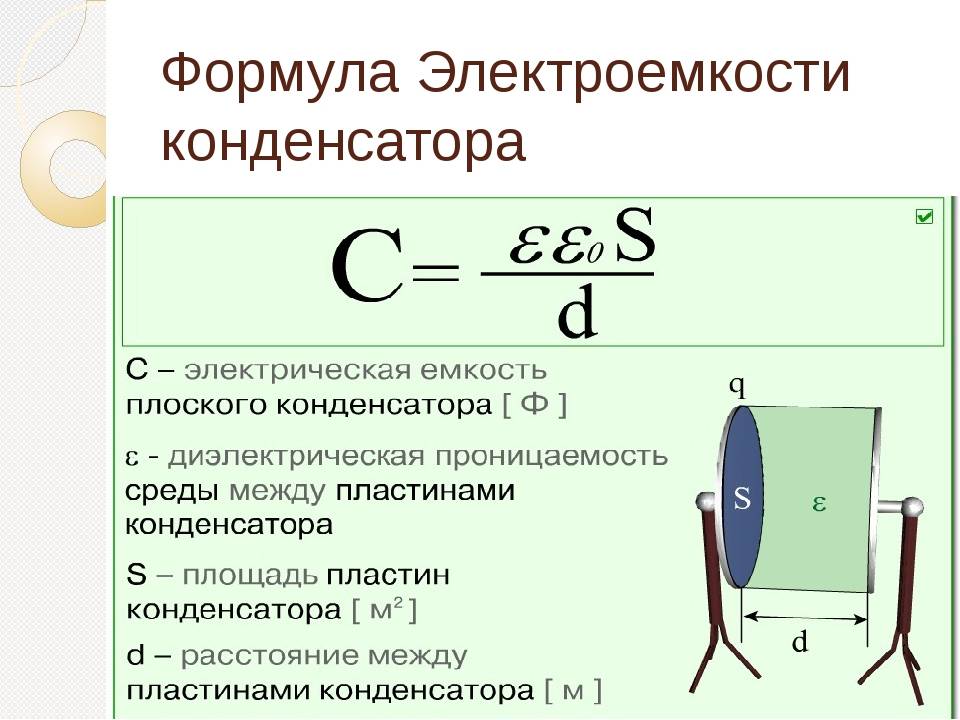
[Емкость конденсатора] = [Диэлектрическая проницаемость вакуума] * [Диэлектрическая проницаемость диэлектрика между пластинами] * [Площадь пластин] / [Расстояние меду пластинами], где [Диэлектрическая проницаемость вакуума] = 8,854187817E-12 Ф/м, [Диэлектрическая проницаемость диэлектрика между пластинами] зависит от конкретных свойств диэлектрического материала. Некоторые вещества, например, слюда, способствуют накоплению энергии, тогда эта константа больше единицы, может быть равна трем и более. Некоторые вещества наоборот препятствуют накоплению энергии, тогда эта константа меньше единицы. Настоящая формула приведена здесь справочно. Инженеру – схемотехнику она никогда не нужна. Емкость конденсатора написана на его корпусе. Этого вполне достаточно.

Напряжение на конденсаторе не может измениться мгновенно. Конденсатор всячески сопротивляется этому. Это необходимо учитывать при проектировании электронных схем. Попытки быстро зарядить или разрядить конденсатор приводят к всплескам электрического тока, которые могут быть опасны для других элементов в схеме.

На идеальном конденсаторе тепловая энергия не выделяется, хотя через него может проходить переменный ток. Дело в том, что сначала конденсатор заряжается, накапливает энергию, потом разряжается, отдает энергию в цепи питания, не рассеивая ее.

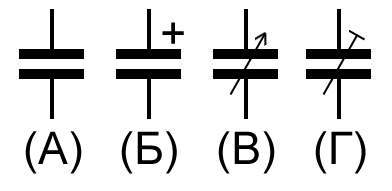
На схемах конденсатор обозначается, как показано на рисунках. (А) – обычный конденсатор, (Б) – электролитический, (В) – переменный, (Г) – подстроечный.

Физика ёмкостных характеристик

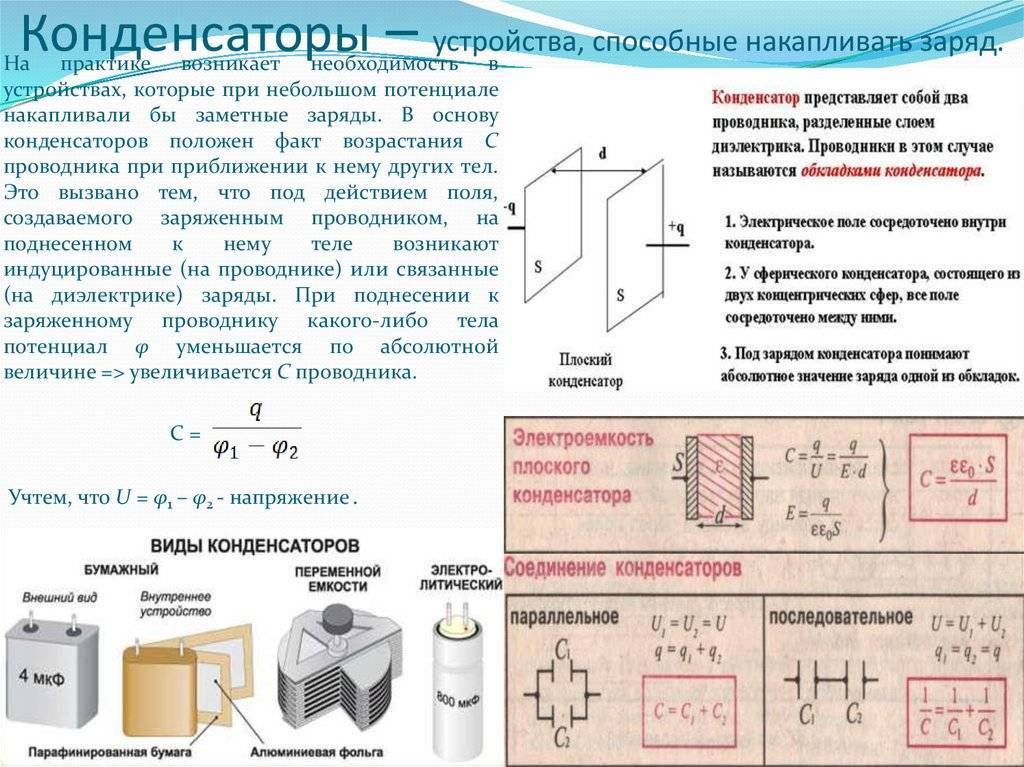
Устройства, обладающие способностью хранения энергии в форме электрического заряда и производящие при этом разность потенциалов, называют конденсаторами. В простейшем виде они состоят из двух или более параллельных проводящих пластин, находящихся на небольшом расстоянии друг от друга, но электрически разделённых либо воздухом, либо каким-либо другим изоляционным материалом, например, вощёной бумагой, слюдой, керамикой, пластмассой или специальным гелем.

Вам это будет интересно Понятие, виды и свойства электрического тока

Если подключить к пластинам источник напряжения, то одна из них получит избыток электронов, а на другой сформируется их дефицит. Ионы и электроны на каждой из этих пластин притягиваются друг к другу, но благодаря диэлектрическому барьеру они не соединяются, а накапливаются на плоскостях проводников. В результате первая пластина (электрод) окажется заряженной отрицательно, а вторая — положительно. Неподвижные заряды создают постоянное электрическое поле, теоретически сохраняемое неограниченное количество времени в незамкнутой электрической цепи.

Поток электронов на пластины называется зарядным током, продолжающим присутствовать до тех пор, пока напряжение на пластинах не сравняется с приложенным. В этот момент конденсатор считается полностью заряженным, то есть зарядов на пластинах становится так много, что они отталкивают вновь поступающие. При подключении к заряженному устройству нагрузки электроны и ионы находят новый путь друг к другу. В этом случае конденсатор работает как источник тока до момента потери разности потенциалов на электродах.

Способность конденсатора хранить заряд Q (измеряется в кулонах) называют ёмкостью. Чем больше площадь пластин и меньше расстояние между ними (благодаря усилению эффекта притяжения зарядов между обкладками), тем большая ёмкость устройства. Степень приближения пластин ограничивается способностью диэлектрика сопротивляться разрядке пробоем между ними. Таким образом, три характеристики определяют производительность конденсатора:

• геометрия пластин;
• расстояние между ними;
• диэлектрический материал между пластинами.

Принцип работы конденсатора

По принципу работы он схож с батарейкой только на первый взгляд, но все же он сильно отличается от него по принципу и скорости заряда-разряда, максимальной емкости.

Заряд конденсатора. В момент подключения к источнику питания оказывается больше всего места на электродах, поэтому и ток будет зарядки максимальным, но по мере накопления заряда, ток будет уменьшаться и пропадет полностью после полного заряда. При зарядке на одной пластине будут собираться отрицательно заряженные частицы- электроны, а на другой – ионы, положительно заряженные частицы. Диэлектрик выступает препятствием для их перескакивания на противоположную сторону конденсатора.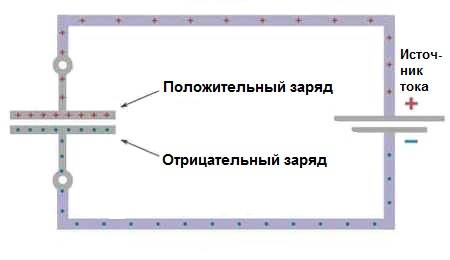При зарядке растет и напряжение с нуля перед началом зарядки и достигает в самом конце максимума, равного напряжению источника питания.

Разрядка конденсатора. Если после окончания зарядки отключить источник питания и подключить нагрузку R, то он сам превратится в источник тока. При подключении нагрузки образовывается цепь между пластинами. Отрицательно заряженные электроны двинуться через нагрузку к положительно заряженных ионам на другой пластине по закону притяжения между разноименными зарядами.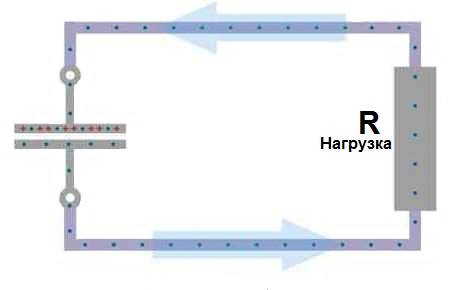В момент подключения нагрузки, начальный ток по закону Ома будет равняться величине напряжения на электродах (равного в конце зарядке конденсатора напряжению источника питания), разделенному на сопротивление нагрузки. После того как пошел ток, конденсатор начинает постепенно терять заряд или разряжаться. Одновременно с этим начнет снижаться величина напряжения, соответственно по закону Ома и ток. В то же время чем выше уровень разряда обкладок, тем ниже будет скорость падения напряжения и силы тока. Процесс завершится после того, как напряжение на электродах конденсатора станет равно нулю.

Время зарядки конденсатора на прямую зависит от величины его емкости. Чем большей она величины, тем дольше будет проходить по цепи большее количество заряда.

Время разрядки зависит от величины подключенной нагрузки. Чем больше подключено сопротивление R, тем меньше будет ток разрядки.

Понятие емкости, правила измерения

Данная величина показывает, какое количество электронов (или других заряженных частиц) должно переместиться от одного объекта к другому для получения необходимого значения напряжения. Последнее возникает по той причине, что при перемещении частиц между объектами образуется разница потенциалов.

Единицей измерения емкостного значения является фарад (на письме обозначается заглавной кириллической литерой Ф). Когда при перенесении заряда в 1 Кулон напряжение меняется на 1 Вольт, значение емкости между перенесенными объектами составляет 1 Фарад. Формула зависимости емкости от напряжения имеет такой вид:

С (емкость) = Q (заряд)/U(напряжение).

Если мастер собрался измерять емкость используемого в радиоэлектронной схеме конденсатора, ему потребуется такой прибор, как мультиметр. С задачей способен справиться даже бюджетный аппарат, при этом наибольшая точность демонстрируется при работе с пленочными конденсаторными элементами. Для максимально точных замеров можно воспользоваться измерителем иммитанса, но данный прибор отличается очень высокой ценой (около 120 тыс. руб.). При использовании мультиметра нужно придерживаться следующего алгоритма:

1. Отсоединить электроцепь от источника нагрузки. Проверить отсутствие питания, установив на устройстве режим замера напряжения и поставив щупы к источнику: показатель должен быть равен нулю.
2. Снять заряд с конденсатора пассивным способом (подождать 20-30 минут) или активным (с помощью резистора). Для маленьких элементов нужен прибор с сопротивлением более 2 кОм. С достаточно крупными конденсаторами (например, в фотоаппаратах и бытовой технике) лучше вообще не работать в домашних условиях без подготовки – они накапливают опасно высокий заряд. Для разрядки такого элемента требуется резистор на 20 кОм и 5 Вт, подсоединенный через изолированный провод диаметром 3,3 мм2, предназначенный для эксплуатации под напряжением до 600 В.
3. Отключить конденсатор от цепи. После этого поставить мультиметр в режим замера емкости. Если прибор снабжен несколькими настроечными диапазонами, нужно поставить тот, что с наибольшей вероятностью окажется верным (сориентироваться можно по маркировке). При наличии клавиши Rel нужно нажать ее, чтобы емкость сошла со щуповых элементов.
4. Щупы помещаются к выводам конденсатора. При тестировании поляризованных элементов надо обязательно соблюдать полярность. Теперь нужно дождаться вывода данных на дисплей. Если высветилось слово overload (или OL), показатель слишком высокий для обнаружения данным прибором или в данном диапазоне (во втором случае нужно выбрать другой диапазон).

Важно! Нельзя подключать мультиметр к конденсаторному элементу, на корпусе которого имеются проколы или выпуклые места. Такие элементы вообще не стоит эксплуатировать – при подключении питания они способны взорваться

Процесс измерения емкости конденсатора мультиметром

Подключение конденсаторов

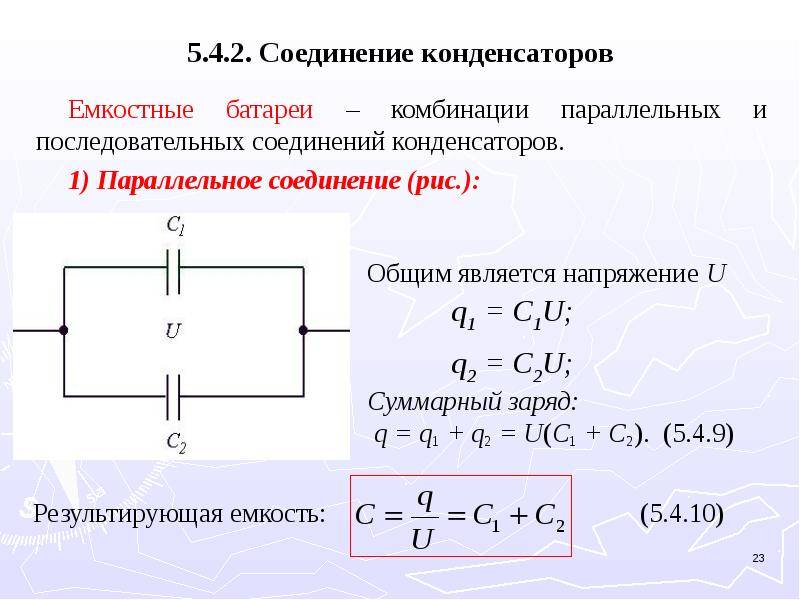
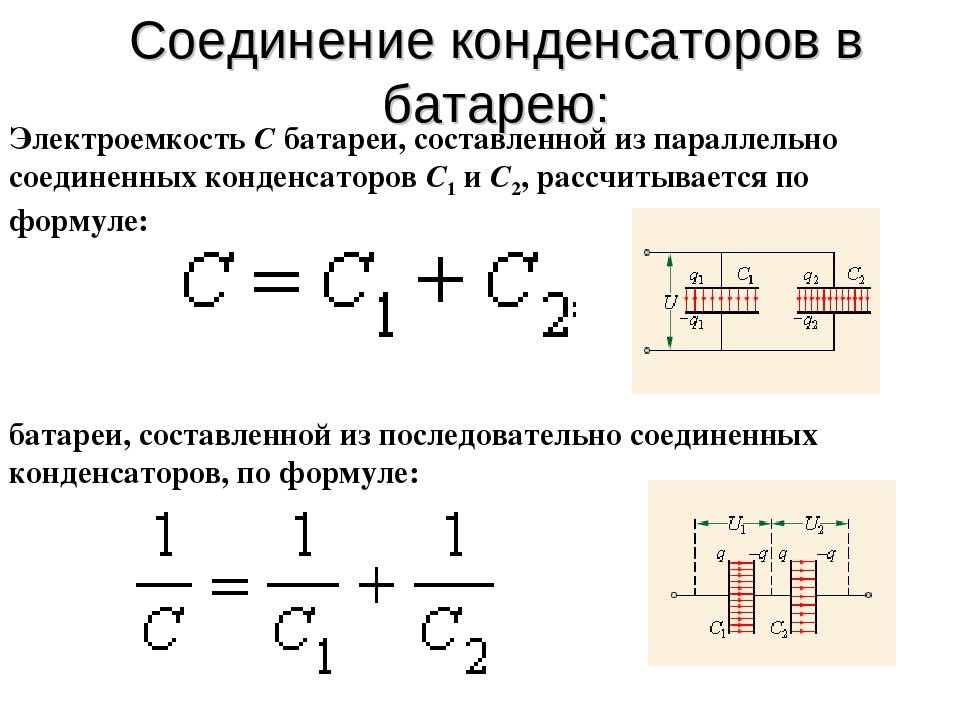
Конденсаторы, как и резисторы, можно подключать последовательно и параллельно. Однако эффекты от этих комбинаций противоположны!

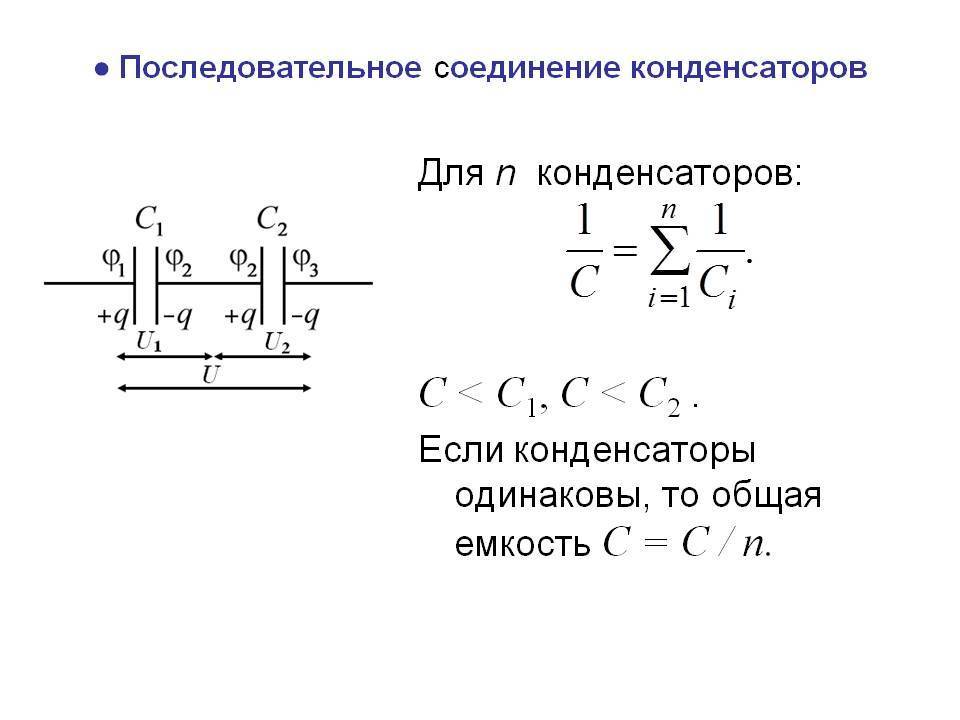
Последовательно соединяют только конденсаторы с емкостью меньше, чем у самого маленького используемого элемента. А конденсаторы с емкостью, большей, чем самая большая из используемых, соединяют параллельно. Формулы для расчета полученных значений несложны, но их стоит иметь под рукой.

Подключение конденсаторов параллельно (слева) и последовательно (справа)

Здесь также следует обращать внимание на количество конденсаторов и стандартизировать их, прежде чем подставлять их в формулу! Стоит помнить о таких возможностях подключения конденсаторов, но на практике это применяется нечасто. Теперь вы можете попробовать протестировать предыдущую схему, вставив на плату параллельно подключенные конденсаторы:

Теперь вы можете попробовать протестировать предыдущую схему, вставив на плату параллельно подключенные конденсаторы:

Пример параллельного подключения конденсаторов

Кстати, некоторые более дорогие мультиметры имеют функцию измерения емкости конденсаторов. Измеряемый конденсатор необходимо предварительно разрядить, путем короткого замыкания его выводов, иначе тестер может выйти из строя! Но, откровенно говоря, с практической точки зрения, эта функция используется очень редко, так что … не придется сожалеть о том, что ее нет.

Виды конденсаторов

Бумажные и металлобумажные конденсаторы

У бумажного конденсатора диэлектриком, разделяющим фольгированные обкладки, является специальная конденсаторная бумага. В электронике бумажные конденсаторы могут применяться как в цепях низкой частоты, так и в высокочастотных цепях.

Хорошим качеством электрической изоляции и повышенной удельной емкостью обладают герметичные металлобумажные конденсаторы, у которых вместо фольги (как в бумажных конденсаторах) используется вакуумное напыление металла на бумажный диэлектрик.

Бумажный конденсатор не имеет большую механическую прочность, поэтому его начинку помещают в металлический корпус, служащий механической основой его конструкции.

Электролитические конденсаторы

В электролитических конденсаторах, в отличии от бумажных, диэлектриком является тонкий слой оксида металла, образованный электрохимическим способом на положительной обложке из того же металла.

Вторую обложку представляет собой жидкий или сухой электролит. Материалом, создающим металлический электрод в электролитическом конденсаторе, может быть, в частности, алюминий и тантал. Традиционно, на техническом жаргоне «электролитом» называют алюминиевые конденсаторы с жидким электролитом.

Но, на самом деле, к электролитическим также относятся и танталовые конденсаторы с твердым электролитом (реже встречаются с жидким электролитом). Почти все электролитические конденсаторы поляризованы, и поэтому они могут работать только в цепях с постоянным напряжением с соблюдением полярности.

В случае инверсии полярности, может произойти необратимая химическая реакция внутри конденсатора, ведущая к разрушению конденсатора, вплоть до его взрыва по причине выделяемого внутри него газа.

Блок питания 0…30В/3A
Набор для сборки регулируемого блока питания…

Подробнее

К электролитическим конденсаторам так же относится, так называемые, суперконденсаторы (ионисторы) обладающие электроемкостью, доходящей порой до нескольких тысяч Фарад.

Алюминиевые электролитические конденсаторы

В качестве положительного электрода используется алюминий. Диэлектрик представляет собой тонкий слой триоксида алюминия (Al₂O₃),

Свойства:

• работают корректно только на малых частотах;
• имеют большую емкость.

Характеризуются высоким соотношением емкости к размеру: электролитические конденсаторы обычно имеют большие размеры, но конденсаторы другого типа, одинаковой емкости и напряжением пробоя были бы гораздо больше по размеру.

Характеризуются высокими токами утечки, имеют умеренно низкое сопротивление и индуктивность.

Танталовые электролитические конденсаторы

Это вид электролитического конденсатора, в котором металлический электрод выполнен из тантала, а диэлектрический слой образован из пентаоксида тантала (Ta₂O₅).

Свойства:

• высокая устойчивость к внешнему воздействию;
• компактный размер: для небольших (от нескольких сотен микрофарад), размер сопоставим или меньше, чем у алюминиевых конденсаторов с таким же максимальным напряжением пробоя;
• меньший ток утечки по сравнению с алюминиевыми конденсаторами.

Полимерные конденсаторы

В отличие от обычных электролитических конденсаторов, современные твердотельные конденсаторы вместо оксидной пленки, используемой в качестве разделителя обкладок, имеют диэлектрик из полимера. Такой вид конденсатора не подвержен раздуванию и утечке заряда.

Физические свойства полимера способствуют тому, что такие конденсаторы отличаются большим импульсным током, низким эквивалентным сопротивлением и стабильным температурным коэффициентом даже при низких температурах.

Полимерные конденсаторы могут заменять электролитические или танталовые конденсаторы во многих схемах, например, в фильтрах для импульсных блоков питания, или в преобразователях DC-DC.

Зависимость электроемкости от площади пластин конденсатора

От чего зависит электроемкость? Начнем с размера пластин.

Зафиксируем полученное в первом опыте с электрометром и конденсатором значение напряжения $U_1$. Теперь возьмем пластины, имеющие большую площадь. Сообщим им точно такой же заряд $q$ (рисунок 9).

Рисунок 9. Зависимость емкости конденсатора от площади его пластин

Мы увидим, что стрелка электрометра отклоняется меньше. Это означает, что напряжение между этими пластинами меньше напряжения между пластинами меньшей площади ($U_1 > U_2$).

Из определения электроемкости:$C_1 = \frac{q}{U_1}$,$C_2 = \frac{q}{U_2}$,$C_2 > C_1$.

{"questions":,"answer":}}}]}

Расстояние между пластинами

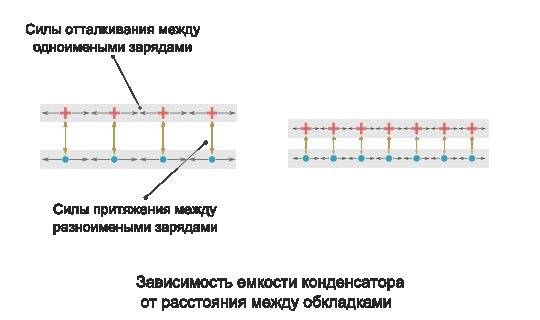
Емкость конденсатора обратно пропорциональна расстоянию между пластинами. Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).

Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.

Характеристики конденсатора

Основной характеристикой данного элемента является емкость, или С. Она определяет способность устройства собирать электрический заряд, зависит от геометрической конфигурации крышек и от электрической проницаемости диэлектрика между крышками.

Важно! Емкость зависит от типа используемого диэлектрика, а также от геометрических размеров элемента. Для того, чтобы описать принцип работы устройства формулой, необходимо понять, что это постоянная пропорциональность в уравнении, представляющая собой взаимную зависимость накопленного заряда q от площади пластинок и от разности потенциалов V между ними

Для того, чтобы описать принцип работы устройства формулой, необходимо понять, что это постоянная пропорциональность в уравнении, представляющая собой взаимную зависимость накопленного заряда q от площади пластинок и от разности потенциалов V между ними.

Вам это будет интересно Особенности поперечного сечения

Мощность выражается в единицах, называемых фарадами F. Но на практике используются и более мелкие единицы, такие как микрофарады и пикофарады.

Внешний вид устройств

Таким образом, если напряжение U приложено к конденсатору, электрический заряд накапливается на крышках детали. Значение накопленного заряда на каждой пластинке одинаково, они отличаются только знаком. Этот процесс накопления электрического показателя на называется зарядкой.

Другим параметром детали является номинальное напряжение, а именно, его максимальное значение, которое может подаваться на конденсатор. При подключении более высокого напряжения возникает пробой диэлектрика. Это приводит к короткому замыканию элемента. Каким будет номинальное значение напряжения, зависит от типа диэлектрика и его толщины.

Важно! Чем толще диэлектрик, тем выше номинальное напряжение, которое он выдерживает. Условные обозначения

Условные обозначения

Ещё одним параметром является ток утечки -значение проводящего показателя, возникающее при подаче постоянного напряжения на концы элемента.

Емкостное и индуктивное сопротивление в цепи переменного тока

Если мы включим конденсатор в цепь постоянного тока, то обнаружим, что он оказывает бесконечно большое сопротивление, поскольку постоянный ток просто не может пройти через диэлектрик между обкладками, так как диэлектрик по определению не проводит постоянный электрический ток.

Конденсатор разрывает цепь постоянного тока. Но если тот же конденсатор включить теперь в цепь переменного тока, то окажется, что ее конденсатор будто бы и не разрывает полностью, он просто попеременно заряжается и разряжается, то есть электрический заряд движется, и ток во внешней цепи поддерживается.

Опираясь на теорию Максвелла, в этом случае можно сказать, что переменный ток проводимости внутри конденсатора все же замыкается, только в данном случае — током смещения. Значит конденсатор в цепи переменного тока выступает неким сопротивлением конечной величины. Такое сопротивление называется емкостным

Практика давно показала, что величина переменного тока, текущего через провод, зависит от формы этого провода и от магнитных свойств среды вокруг него. При прямом проводе ток будет наибольшим, а если этот же провод свернуть в катушку с большим количеством витков, то величина тока окажется меньше.

А если в ту же катушку еще и ввести ферромагнитный сердечник, то ток еще сильнее уменьшится. Следовательно проводник оказывает переменному току не только омическое (активное) сопротивление, но еще и некое дополнительное сопротивление, зависящее от индуктивности проводника. Данное сопротивление называется индуктивным

Его физический смысл состоит в том, что изменяющийся ток в проводнике, обладающем некой индуктивностью, инициирует в этом проводнике ЭДС самоиндукции, стремящуюся препятствовать изменениям тока, то есть стремящуюся уменьшить ток. Это равносильно увеличению сопротивления проводника.

Емкостное сопротивление в цепи переменного тока

Для начала поговорим более подробно о емкостном сопротивлении. Допустим, что конденсатор емкостью С подключен к источнику синусоидального переменного тока, тогда ЭДС этого источника будет описываться следующей формулой:

Падением напряжения на соединительных проводах пренебрежем, так как оно обычно очень мало, а при необходимости его можно будет рассмотреть отдельно. Примем сейчас, что напряжение на обкладках конденсатора равно напряжению источника переменного тока. Тогда:

В любой момент времени заряд на конденсаторе зависит от его емкости и от напряжения между его обкладками. Тогда для данного известного источника, о котором говорилось выше, получим выражение для нахождения заряда на обкладках конденсатора через напряжение источника:

Пусть за бесконечно малое время dt заряд на конденсаторе изменяется на величину dq, тогда по проводам от источника к конденсатору потечет ток I, равный:

Амплитудное значение тока окажется равно:

Тогда окончательное выражение для тока будет иметь вид:

Перепишем формулу для амплитуды тока в следующем виде:

Данное соотношение есть закон Ома, где величина обратная произведению угловой частоты на емкость играет роль сопротивления, и по сути являет собой выражение для нахождения емкостного сопротивления конденсатора в цепи синусоидального переменного тока:

Значит емкостное сопротивление обратно пропорционально угловой частоте тока и емкости конденсатора. Легко понять и физический смысл данной зависимости.

Чем больше емкость конденсатора в цепи переменного тока и чем чаще изменяется направление тока в этой цепи, тем в конце концов больший суммарный заряд проходит за единицу времени через поперечное сечение проводов, соединяющих конденсатор с источником переменного тока. Значит ток пропорционален произведению емкости и угловой частоты.

Для примера выполним расчет емкостного сопротивления конденсатора электроемкостью 10 мкф для цепи синусоидального переменного тока с частотой 50 Гц:

Если бы частота была 5000 Гц, то тот же самый конденсатор представлял бы собой сопротивление около 3 Ом.

Из приведенных выше формул ясно, что ток и напряжение в цепи переменного тока с конденсатором всегда изменяются в разных фазах. Фаза тока опережает фазу напряжения на пи/2 (90 градусов). А значит максимум тока во времени существует всегда на четверть периода раньше, чем максимум напряжения. Таким образом на емкостном сопротивлении ток опережает напряжение на четверть периода по времени или на 90 градусов по фазе.